题目内容
16. 如图,梯形ABCD中AD∥BC,AB=DC,AE=GF=GC
如图,梯形ABCD中AD∥BC,AB=DC,AE=GF=GC(1)求证:四边形AEFG是平行四边形;
(2)当∠FGC=2∠EFB时,求证:四边形AEFG是矩形.
分析 (1)首先证明∠B=∠GFC=∠C,根据平行线的判定可得GF∥AB,再由GF=AE,可得四边形AEFG是平行四边形;
(2)过G作GM⊥BC垂足为M,根据等腰三角形的性质可得∠FGC=2∠FGM,然后再证明∠EFG=90°,可得四边形AEFG是矩形.
解答 证明:(1)在梯形ABCD中,
∵AB=CD,
∴∠B=∠C,
∵GF=GC,
∴∠GFC=∠C,
∴∠B=∠GFC,
∴GF∥AB,
∵GF=AE,
∴四边形AEFG是平行四边形;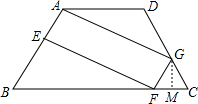
(2)过G作GM⊥BC垂足为M,
∵GF=GC,
∴∠FGC=2∠FGM,
∵∠FGC=2∠EFB,
∴∠FGM=∠EFB,
∵∠FGM+∠GFM=90°,
∴∠EFB+∠GFM=90°,
∴∠EFG=90°,
∴平行四边形AEFG为矩形.
点评 此题主要考查了矩形的判定和平行四边形的判定,关键是掌握一组对边平行且相等的四边形是平行四边形,一个角是直角的平行四边形是矩形.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
6.已知A(-2,3),则A点关于原点的对称点的坐标为( )
| A. | (-2,3) | B. | (2,3) | C. | (-2,-3) | D. | (2,-3) |
1. 如图,在△ABC中,∠A=60°,∠C=50°,BD是∠ABC的角平分线,点E在AB上,且ED∥BC,则∠1的度数是( )
如图,在△ABC中,∠A=60°,∠C=50°,BD是∠ABC的角平分线,点E在AB上,且ED∥BC,则∠1的度数是( )
 如图,在△ABC中,∠A=60°,∠C=50°,BD是∠ABC的角平分线,点E在AB上,且ED∥BC,则∠1的度数是( )
如图,在△ABC中,∠A=60°,∠C=50°,BD是∠ABC的角平分线,点E在AB上,且ED∥BC,则∠1的度数是( )| A. | 35° | B. | 30° | C. | 25° | D. | 60° |
8.若关于x的不等式组$\left\{\begin{array}{l}{9-2x>1}\\{x-m≥1}\end{array}\right.$有6个整数解,则m的取值范围是( )
| A. | -4<m≤-3 | B. | -3≤m<-2 | C. | -4≤m<-3 | D. | -3<m≤-2 |
5.已知1纳米=$\frac{1}{1{0}^{9}}$,那么$\frac{1}{1{0}^{9}}$用科学记数法表示为( )
| A. | 1.0×109 | B. | 1.0×10-9 | C. | -1.0×109 | D. | -1.0×10-9 |