题目内容
12.小明的数学探究小组进行了系列探究活动.类比定义:类比等腰三角形给出如下定义:有一组邻边相等的凸四边形叫做邻等四边形.
探索理解:
(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请你协助小明用两种不同的方法画出格点D,连接DA、DC,使四边形ABCD为邻等四边形;
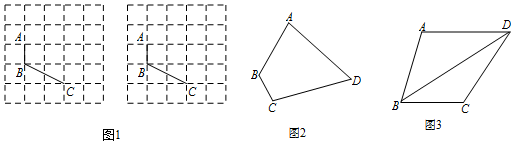
尝试体验:
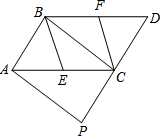
(2)如图2,邻等四边形ABCD中,AD=CD,∠ABC=120°,∠ADC=60°,AB=2,BC=1,求四边形ABCD的面积.
解决应用:
(3)如图3,邻等四边形ABCD中,AD=CD,∠ABC=75°,∠ADC=60°,BD=4.
小明爸爸所在的工厂,需要裁取某种四边形的材料板,这个材料板的形状恰巧是符合如图3条件的邻等四边形,要求尽可能节约.你能求出这种四边形面积的最小值吗?如果能,请求出此时四边形ABCD面积的最小值;如果不能,请说明理由.
分析 (1)如图1所示;根据邻等四边形的定义作出图形即可.
(2)如图2中,连接AC,作CH⊥AB于H.在Rt△BCH中,求出BH=$\frac{1}{2}$BC=$\frac{1}{2}$,HC=$\sqrt{3}$BH=$\frac{\sqrt{3}}{2}$,在Rt△ACH中,AC2=AH2+CH2=(2+$\frac{1}{2}$)2+($\frac{\sqrt{3}}{2}$)2=7,分别求出△ABC,△ADC的面积即可解决问题.
(3)能.因为△ADC是等边三角形,所以可以将△BDC绕点D顺时针旋转60°得到△HDA,连接BH.由S四边形ABCD=S△ADH+S△ABD=S△DBH-S△ABH,可知当△ABH面积最大时,四边形ABCD的面积最小,只要求出△ABH的面积的最大值即可解决问题.
解答 解:(1)如图1,
邻等四边形ABCD即为所求.
(2)如图2中,连接AC,作CH⊥AB于H.
在Rt△BCH中,∵BC=1,∠CBH=180°-∠ABC=180°-120°=60°,
∴BH=$\frac{1}{2}$BC=$\frac{1}{2}$,HC=$\sqrt{3}$BH=$\frac{\sqrt{3}}{2}$,
在Rt△ACH中,AC2=AH2+CH2=(2+$\frac{1}{2}$)2+($\frac{\sqrt{3}}{2}$)2=7,
∴S△ABC=$\frac{1}{2}$•AB•CH=$\frac{\sqrt{3}}{2}$,
∴AD=DC,∠ADC=60°,
∴△ADC是等边三角形,
∴S△ACD=$\frac{\sqrt{3}}{4}$AC2=$\frac{7\sqrt{3}}{4}$,
∴S四边形ABCD=S△ACB+S△ADC=$\frac{9\sqrt{3}}{4}$.
(3)能.如图3中,∵AD=DC,∠ADC=60°,
∴△ADC是等边三角形,将△BDC绕点D顺时针旋转60°得到△HDA,连接BH.
∵DB=DH,∠HDB=60°,
∴△HDB是等边三角形,
∴S四边形ABCD=S△ADH+S△ABD=S△DBH-S△ABH,
∴当△ABH面积最大时,四边形ABCD的面积最小,
∵∠ABC=75°,∠ADC=60°,
∴∠BAD+∠BCD=∠BAD+∠DAH=360°-75°-60°=225°,
∴∠BAH=135°,
∵BH=DB=4,
∴点A在定圆⊙O上运动,当O、A、D共线时,△ABH的面积最大,此时OD⊥BH,设OA交BH于K,则HK=KB=2,
∵AH=AB,
∴∠AHB=∠ABH=22.5°,在HK上取一点F,使得FH=FA,则△AKF是等腰直角三角形,设AK=FK=x,则FH=AF=$\sqrt{2}$x,
∴2=x+$\sqrt{2}$x,
∴x=2$\sqrt{2}$-2,
∴△ABH的面积最大值=$\frac{1}{2}$•4•(2$\sqrt{2}$-2)=4$\sqrt{2}$-4,
∴四边形ABCD的面积的最小值=$\frac{\sqrt{3}}{4}$×42-(4$\sqrt{2}$-4)=4$\sqrt{3}$-4$\sqrt{2}$+4.
点评 本题考查四边形综合题、等边三角形的判定和性质、三角形的面积、勾股定理,30度直角三角形的性质、圆等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用辅助圆解决最值问题,属于中考压轴题.

 如图,在平行四边形ABDC中,分别取AC、BD的中点E和F,连接BE、CF,过点A作AP∥BC,交DC的延长线于点P.
如图,在平行四边形ABDC中,分别取AC、BD的中点E和F,连接BE、CF,过点A作AP∥BC,交DC的延长线于点P. 如图,有一块直角三角形纸片,两直角边AC=9cm,BC=12cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长?
如图,有一块直角三角形纸片,两直角边AC=9cm,BC=12cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长?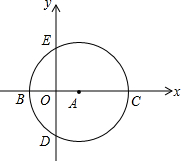 如图,在直角坐标系中,以点A(3,0)为圆心,以5为半径作圆与x轴相交于点B,C,与y轴相交于点D,E.
如图,在直角坐标系中,以点A(3,0)为圆心,以5为半径作圆与x轴相交于点B,C,与y轴相交于点D,E.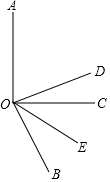 如图,∠AOC=90°,∠BOC=60°,OE平分∠BOC,OD平分∠AOB.求:
如图,∠AOC=90°,∠BOC=60°,OE平分∠BOC,OD平分∠AOB.求: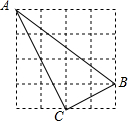 如图:正方形网格中每个小方格的边长为1,且点A、B、C均为格点.
如图:正方形网格中每个小方格的边长为1,且点A、B、C均为格点.