题目内容
1.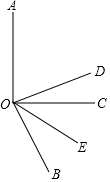 如图,∠AOC=90°,∠BOC=60°,OE平分∠BOC,OD平分∠AOB.求:
如图,∠AOC=90°,∠BOC=60°,OE平分∠BOC,OD平分∠AOB.求:(1)∠DOE度数;
(2)若∠BOC=α(0<α<90°),其他条件不变,∠DOE的度数是多少?
分析 (1)根据∠AOC、∠BOC的度数可得出∠AOB的度数,根据角平分线的定义即可得出∠BOE、∠BOD的度数,再根据∠DOE与∠BOE、∠BOD之间的关系通过角的计算即可得出结论;
(2)根据∠AOC、∠BOC的度数可得出∠AOB的度数,根据角平分线的定义即可得出∠BOE、∠BOD的度数,再根据∠DOE与∠BOE、∠BOD之间的关系通过角的计算即可得出结论;
解答 解:(1)∵∠AOC=90°,∠BOC=60°,
∴∠AOB=∠AOC+∠BOC=150°.
∵OE平分∠BOC,OD平分∠AOB,
∴∠BOE=$\frac{1}{2}$∠BOC=30°,∠BOD=$\frac{1}{2}$∠AOB=75°,
∴∠DOE=∠BOD-∠BOE=45°.
(2)∵∠AOC=90°,∠BOC=α,
∴∠AOB=∠AOC+∠BOC=90°+α.
∵OE平分∠BOC,OD平分∠AOB,
∴∠BOE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$α,∠BOD=$\frac{1}{2}$∠AOB=45°+$\frac{1}{2}$α,
∴∠DOE=∠BOD-∠BOE=45°.
点评 本题考查了角的计算以及平分线的定义,解题的关键是:(1)找出∠BOE、∠BOD的度数;(2)找出∠BOE、∠BOD的度数.

练习册系列答案
相关题目
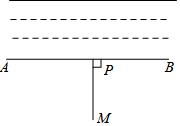 如图,计划把河水引到水池M中,先引MP⊥AB,垂足为P,然后沿MP开渠,能使所开的渠道最短,这样设计的依据是垂线段最短.
如图,计划把河水引到水池M中,先引MP⊥AB,垂足为P,然后沿MP开渠,能使所开的渠道最短,这样设计的依据是垂线段最短.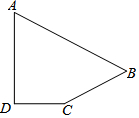 在四边形ABCD中,∠D=90°,AD=$\sqrt{12}$,CD=2,BC=3,AB=5,求:四边形ABCD的面积.
在四边形ABCD中,∠D=90°,AD=$\sqrt{12}$,CD=2,BC=3,AB=5,求:四边形ABCD的面积.