题目内容
在△ABC中,AB=15,BC=10,CA=20,点O是△ABC内角平分线的交点,则△ABO,△BCO,△CAO的面积比是 .
考点:角平分线的性质
专题:
分析:首先过点O,作OD⊥AB于D,作OE⊥AC于E,作OF⊥BC于F,由点O是△ABC内角平分线的交点,根据角平分线的性质,即可得OD=OE=OF,继而可得S△ABO:S△BCO:S△CAO=AB:BC:CA,则可求得答案.
解答: 解:过点O,作OD⊥AB于D,作OE⊥AC于E,作OF⊥BC于F,
解:过点O,作OD⊥AB于D,作OE⊥AC于E,作OF⊥BC于F,
∵点O是△ABC内角平分线的交点,
∴OD=OE=OF,
∴S△ABO=
AB•OD,S△CAO=
AC•OE,S△BCO=
BC•OF,
∵AB=15,BC=10,CA=20,
∴S△ABO:S△BCO:S△CAO=AB:BC:CA=10:15:20=3:2:4.
故答案为:3:2:4.
 解:过点O,作OD⊥AB于D,作OE⊥AC于E,作OF⊥BC于F,
解:过点O,作OD⊥AB于D,作OE⊥AC于E,作OF⊥BC于F,∵点O是△ABC内角平分线的交点,
∴OD=OE=OF,
∴S△ABO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=15,BC=10,CA=20,
∴S△ABO:S△BCO:S△CAO=AB:BC:CA=10:15:20=3:2:4.
故答案为:3:2:4.
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
下列说法中,正确的有( )
①无限小数都是无理数;②无理数都是无限小数;
③带根号的数都是无理数;④-3是9的一个平方根.
①无限小数都是无理数;②无理数都是无限小数;
③带根号的数都是无理数;④-3是9的一个平方根.
| A、0个 | B、1个 | C、2个 | D、3个 |
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若AB=10,CD=8,则OP=
如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若AB=10,CD=8,则OP= 如图,BD是△ABC的角平分线,DE⊥AB,垂足为E.BD=10,BE=8,BC=9,求△BCD的面积.
如图,BD是△ABC的角平分线,DE⊥AB,垂足为E.BD=10,BE=8,BC=9,求△BCD的面积.
 如图,AB为⊙O直径,∠BAC的平分线交⊙O于D点,∠BAC=50°,则∠ABD=
如图,AB为⊙O直径,∠BAC的平分线交⊙O于D点,∠BAC=50°,则∠ABD=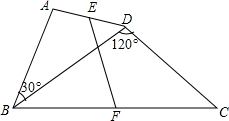 如图,四边形ABCD中,AB=10,CD=8,∠ABD=30°,∠BDC=120°,E,F分别是AD、BC的中点,求EF的长.
如图,四边形ABCD中,AB=10,CD=8,∠ABD=30°,∠BDC=120°,E,F分别是AD、BC的中点,求EF的长.