Question

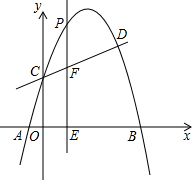已知抛物线y=-x²+

7

2

x+2与直线y=

1

2

x+2相交于点C和D，点P是抛物线在第一象限内的点，它的横坐标为m，过点P作PE⊥x轴，交CD于点F．
（1）求点C和D的坐标；
（2）求抛物线与x轴的交点坐标；
（3）如果以P、C、O、F为顶点的四边形是平行四边形，求m的值．

Answer 1

考点：二次函数综合题

专题：

分析：（1）解抛物线和直线的解析式组成的方程组即可；
（2）令y=0，解一元二次方程即可；
（3）若四边形PCOF是平行四边形，则PF=OC=2，先化简题意表示出点P的坐标为（m，-m²+

7

2

m+2），点F的坐标为（m，

1

2

m+2），然后分两种情况讨论求得；

解答：解：（1）解

y=-x2+ 7 2 x+2 y= 1 2 x+2

则-x2+

7

2

x+2=

1

2

x+2，
整理得，x²-3x=0，解得x₁=0，x₂=3，
∴

x1=0 y1=2

，

x2=3 y2= 7 2

．
∴所求的点的坐标是C（0，2）和D（3，

7

2

）；                       

（2）令y=0，则-x2+

7

2

x+2=0，
解得，x1=-

1

2

，x₂=4，
∴抛物线与x轴的交点坐标为（-

1

2

，0），（4，0）；

（3）若四边形PCOF是平行四边形，则PF=OC=2，
∵点P的横坐标为m，
∴点P的坐标为（m，-m²+

7

2

m+2），点F的坐标为（m，

1

2

m+2），
当0＜m＜3时，PF=（-m²+

7

2

m+2）-（

1

2

m+2），
∴-m²+3m=2，m²-3m+2=0，m₁=1，m₂=2；                 
当3＜p＜4时，PF=（

1

2

m+2）-（-m²+

7

2

m+2），
∴m²-3m=2，m²-3m-2=0，m₃=

3+ 17

2

，m₄=

3- 17

2

（舍去）．    
∴如果以P、C、O、F为顶点的四边形是平行四边形，则m的值为1、2或

3+ 17

2

．

点评：本题考查一次函数和二次函数图象的交点坐标以及抛物线与x轴的交点坐标的求法，平行四边形的和性质，熟练掌握函数和方程的关系是解题的关键．