题目内容
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,且抛物线经过B(1,0)、C(0,-3)两点,与x轴交于另一点A.
(1)求这条抛物线所对应的函数关系式,并求出顶点坐标D.
(2)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<3)与此图象有两个公共点时,b的取值范围.
(3)若P为对称轴x=-1上的一个动点.
①是否存在这样的点P,使得∠APC=90°?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由;
②设抛物线的对称轴交x轴于点M,动点P从点M出发,第1秒以每秒1个单位的速度向上运动,第2秒以每秒2个单位的速度向下运动,第3秒以每秒3个单位的速度向上运动,按此规律一直运动下去…设运动时间为t(秒),试求出:在点P的运动过程中,当△BCP的周长前3次取得最小值时,相应的t的值.
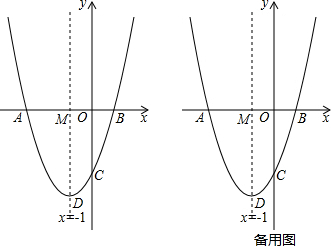
(1)求这条抛物线所对应的函数关系式,并求出顶点坐标D.
(2)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<3)与此图象有两个公共点时,b的取值范围.
(3)若P为对称轴x=-1上的一个动点.
①是否存在这样的点P,使得∠APC=90°?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由;
②设抛物线的对称轴交x轴于点M,动点P从点M出发,第1秒以每秒1个单位的速度向上运动,第2秒以每秒2个单位的速度向下运动,第3秒以每秒3个单位的速度向上运动,按此规律一直运动下去…设运动时间为t(秒),试求出:在点P的运动过程中,当△BCP的周长前3次取得最小值时,相应的t的值.

考点:二次函数综合题
专题:
分析:(1)应用待定系数法即可求得解析式;
(2)画出翻转后新的函数图象,由直线y=x+b,b<3确定出直线移动的范围,求出b的取值范围.
(3)①设P(-1,n),则PM=n,CE=3+n,AM=2,PE=1,根据△APM∽△CPE对应边成比例则
=
即可求得;
②根据轴对称的性质,先确定出P点,然后求得P的坐标,根据题意即可确定t的值.
(2)画出翻转后新的函数图象,由直线y=x+b,b<3确定出直线移动的范围,求出b的取值范围.
(3)①设P(-1,n),则PM=n,CE=3+n,AM=2,PE=1,根据△APM∽△CPE对应边成比例则
| PM |
| PE |
| AM |
| CE |
②根据轴对称的性质,先确定出P点,然后求得P的坐标,根据题意即可确定t的值.
解答: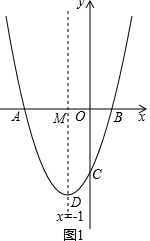 解(1)∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,且抛物线经过B(1,0)、C(0,-3)两点,
解(1)∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,且抛物线经过B(1,0)、C(0,-3)两点,
∴
,
解得
.
∴抛物线的解析式为:y=x2+2x-3.

(2)∵抛物线的解析式为:y=x2+2x-3,
令y=0,则x2+2x-3=0,解得:x=1,x=-3,
∴A(-3,0),
如图2,当直线y=x+b经过A(-3,0)时-3+b=0,可得b=3,又因为b<3,
故可知y=x+b在y=x+3的下方,
当直线y=x+b经过点B(1,0)时,1+b=0,则b=-1,
由图可知符合题意的b的取值范围为-1<b<3时,直线y=x+b(b<3)与此图象有两个公共点.
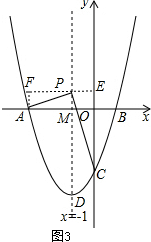
(3)①如图3,设P(-1,n),∵OA=3,OC=3,OM=1,
∴PM=n,CE=3+n,AM=2,PE=1,
∵△APM∽△CPE,
∴
=
,
∴
=
,
解得:n=
,n=
,
∴P(-1,
)或P(-1,
);

②如图4,∵对称轴为x=-1,C(0,-3),
∴C的对称点C′(-2,-3),
设直线BC′的解析式为:y=kx+b,∵B(1,0)、C′(-2,-3),
∴
,
解得
.
∴直线BC′的解析式为:y=x-1,
把x=-1代入得:y=-2,
∴P(-1,-2),
第一次取得最小值是第4秒,
之后第6秒内会第二次经过P点,即5+
=
,
之后第7秒内会第三次经过P点,即6+
=
,
∴根据题意,当△BCP的周长前3次取得最小值时的t的值为:4、
、
.
 解(1)∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,且抛物线经过B(1,0)、C(0,-3)两点,
解(1)∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,且抛物线经过B(1,0)、C(0,-3)两点,∴
|
解得
|
∴抛物线的解析式为:y=x2+2x-3.

(2)∵抛物线的解析式为:y=x2+2x-3,
令y=0,则x2+2x-3=0,解得:x=1,x=-3,
∴A(-3,0),
如图2,当直线y=x+b经过A(-3,0)时-3+b=0,可得b=3,又因为b<3,
故可知y=x+b在y=x+3的下方,
当直线y=x+b经过点B(1,0)时,1+b=0,则b=-1,
由图可知符合题意的b的取值范围为-1<b<3时,直线y=x+b(b<3)与此图象有两个公共点.

(3)①如图3,设P(-1,n),∵OA=3,OC=3,OM=1,
∴PM=n,CE=3+n,AM=2,PE=1,
∵△APM∽△CPE,
∴
| PM |
| PE |
| AM |
| CE |
∴
| n |
| 1 |
| 2 |
| n+3 |
解得:n=
-3+
| ||
| 2 |
-3-
| ||
| 2 |
∴P(-1,
-3+
| ||
| 2 |
-3-
| ||
| 2 |

②如图4,∵对称轴为x=-1,C(0,-3),
∴C的对称点C′(-2,-3),
设直线BC′的解析式为:y=kx+b,∵B(1,0)、C′(-2,-3),
∴
|
解得
|
∴直线BC′的解析式为:y=x-1,
把x=-1代入得:y=-2,
∴P(-1,-2),
第一次取得最小值是第4秒,
之后第6秒内会第二次经过P点,即5+
| 5 |
| 6 |
| 35 |
| 6 |
之后第7秒内会第三次经过P点,即6+
| 1 |
| 7 |
| 43 |
| 7 |
∴根据题意,当△BCP的周长前3次取得最小值时的t的值为:4、
| 35 |
| 6 |
| 43 |
| 7 |
点评:本题考查了待定系数法求解析式,以及根据三角形相似求点的坐标和直线与图象的交点问题,综合体现了数形结合的思想.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
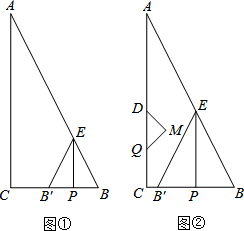 如图①,在直角△ABC中,∠C=90°,AC=8cm,BC=4cm.动点P在线段BC上以1cm/s的速度从点B运动到点C.过点P作PE⊥BC与AB交于点E,以PE为对称轴将PE右侧的图形翻折得到△B′PE,设点P的运动时间为x(s).
如图①,在直角△ABC中,∠C=90°,AC=8cm,BC=4cm.动点P在线段BC上以1cm/s的速度从点B运动到点C.过点P作PE⊥BC与AB交于点E,以PE为对称轴将PE右侧的图形翻折得到△B′PE,设点P的运动时间为x(s).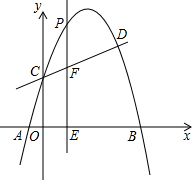 已知抛物线y=-x2+
已知抛物线y=-x2+
 某电信公司开设了甲、乙两种市内移动通信业务.甲种使用者每月需缴18元月租费,然后每通话1分钟,再付话费0.2元;乙种使用者不缴月租费,每通话1分钟,付话费0.6元.若一个月内通话时间为x分钟,甲、乙两种的费用分别为y1和y2元.
某电信公司开设了甲、乙两种市内移动通信业务.甲种使用者每月需缴18元月租费,然后每通话1分钟,再付话费0.2元;乙种使用者不缴月租费,每通话1分钟,付话费0.6元.若一个月内通话时间为x分钟,甲、乙两种的费用分别为y1和y2元.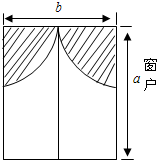 小明房间窗户的装饰物如图所示,它们由两个四分之一圆组成(半径相同,π取3)
小明房间窗户的装饰物如图所示,它们由两个四分之一圆组成(半径相同,π取3) 要使图中的展开图折叠成正方体后,相对面上两个数之和为5,x=
要使图中的展开图折叠成正方体后,相对面上两个数之和为5,x=