题目内容
11.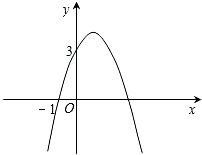 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).(1)写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.
分析 (1)把(-1,0)和(0,3)分别代入y=-x2+bx+c中得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
(2)先求出抛物线与x轴的交点坐标,然后利用图象找出抛物线在x轴上方所对应的自变量的范围即可.
解答 解:(1)根据题意得$\left\{\begin{array}{l}{-1-b+c=0}\\{c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
所以二次函数解析式为y=-x2+2x+3;
(2)当y=0时,-x2+2x+3=0,
解得x1=-1,x2=3,
则抛物线与x轴的两交点坐标为(-1,0),(3,0),
所以当-1<x<3时,y>0.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.也考查了二次函数与不等式(组).

练习册系列答案
相关题目
1.下列总有意义的分式是( )
| A. | $\frac{{{x^2}-{y^2}}}{x-y}$ | B. | $\frac{x+y}{{{x^2}+{y^2}}}$ | C. | $\frac{2x}{{{x^2}+1}}$ | D. | $\frac{{{x^2}+x}}{x+1}$ |
16.中国的领水面积约为370000km2,将数370000用科学记数法表示为( )
| A. | 37×104 | B. | 3.7×104 | C. | 0.37×106 | D. | 3.7×105 |
3.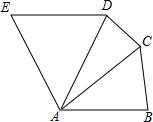 如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
 如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )| A. | 150° | B. | 160° | C. | 130° | D. | 60° |
11.如果a是负数,那么9a2的平方根是( )
| A. | 3a | B. | -3a | C. | ±3a | D. | ±3$\sqrt{a}$ |
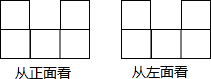 桌上摆着一个由若干个相同正方体组成的几何体,其从正面看和从左面看得到的形状如图所示,那么这个几何体最多可以由13个正方体组成,最少可以由5个正方体组成.
桌上摆着一个由若干个相同正方体组成的几何体,其从正面看和从左面看得到的形状如图所示,那么这个几何体最多可以由13个正方体组成,最少可以由5个正方体组成.