题目内容
6. 如图,OA∥CD,且分别交直线EF于O、F两点,直线GH经过O点且平分
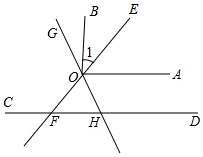
如图,OA∥CD,且分别交直线EF于O、F两点,直线GH经过O点且平分∠AOF,交直线CD于H,OB⊥OA.
(1)若∠1=50°,求∠AOE,∠OHF;
(2)若∠BOG+∠AOF=146°,试求∠1的度数.
分析 (1)由OB⊥OA,得到∠AOB=90°,求得∠AOE=40°,根据平行线的性质得到∠OFH=∠AOE=40°,∠AOH=∠OHF,根据角平分线的定义得到∠AOH=∠FOH,于是得到结论;
(2)根据角平分线的定义得到∠AOH=∠FOH,推出∠BOG+2(∠1+∠BOG)=146°,①由OB⊥OA,得到∠1+∠AOE=90°,得到∠BOG=$\frac{1}{2}$(90°-∠1),②,把②代入①得即可得到结论.
解答 解:(1)∵OB⊥OA,
∴∠AOB=90°,
∵∠1=50°,
∴∠AOE=40°,
∵OA∥CD,
∴∠OFH=∠AOE=40°,∠AOH=∠OHF,
∵GH平分∠AOF,
∴∠AOH=∠FOH,
∴∠FOH=∠FHO=$\frac{1}{2}$(180°-40°)=70°;
(2)∵GH平分∠AOF,
∴∠AOH=∠FOH,
∵∠EOG=∠FOH,
∴∠BOG+∠1=∠FOH=∠AOH,
∵∠BOG+∠AOF=146°,
∴∠BOG+2(∠1+∠BOG)=146°,①
∵OB⊥OA,
∴∠1+∠AOE=90°,
∴∠1=90°-(180°-∠AOF)=2(∠1+∠BOG)-90°,
∴∠BOG=$\frac{1}{2}$(90°-∠1),②,
∴把②代入①得,$\frac{3}{2}$(90°-∠1)+2∠1=146°,
解得:∠1=22°.
点评 本题考查了平行线的性质,角平分线的定义,垂直的定义,能灵活运用平行线的性质进行推理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在下列代数式中,次数为3的单项式是( )
| A. | 3x2 | B. | -x2y | C. | x3+1 | D. | x3y |
15.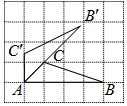 如图,△ABC的三个顶点都在正方形网格的格点处,若将△ABC绕点A逆时针旋转得到△A′B′C′,则tanB′的值为( )
如图,△ABC的三个顶点都在正方形网格的格点处,若将△ABC绕点A逆时针旋转得到△A′B′C′,则tanB′的值为( )
 如图,△ABC的三个顶点都在正方形网格的格点处,若将△ABC绕点A逆时针旋转得到△A′B′C′,则tanB′的值为( )
如图,△ABC的三个顶点都在正方形网格的格点处,若将△ABC绕点A逆时针旋转得到△A′B′C′,则tanB′的值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
16.若不等式组$\left\{\begin{array}{l}{x>1}\\{x<a}\end{array}\right.$无解,则a的取值范围是( )
| A. | a>1 | B. | a≥1 | C. | a<1 | D. | a≤1 |
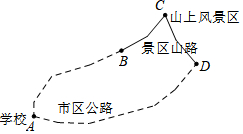 为了提倡“原色青春,绿色行走!”,某市某校组织学生从学校(点A)出发,沿A→B→C→D→A的路线参加总路程为14km绿色行走活动,其中路线A→B段、D→A段是我市区公路,B→C段、C→D段是景区山路.已知学生队伍在市区公路的行进速度为6km/h,在景区山路的行进速度为2km/h,本次行走共用3.5h.问本次行走活动中市区公路、景区山路各多少km?
为了提倡“原色青春,绿色行走!”,某市某校组织学生从学校(点A)出发,沿A→B→C→D→A的路线参加总路程为14km绿色行走活动,其中路线A→B段、D→A段是我市区公路,B→C段、C→D段是景区山路.已知学生队伍在市区公路的行进速度为6km/h,在景区山路的行进速度为2km/h,本次行走共用3.5h.问本次行走活动中市区公路、景区山路各多少km? 如图,∠1=13°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为103°.
如图,∠1=13°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为103°.