题目内容
11. 如图,点E、F位于正方形ABCD边BC、CD上,且BE:EC=2:1,∠EAF=30°,则CF:FD=$\frac{1+13\sqrt{3}}{23}$.
如图,点E、F位于正方形ABCD边BC、CD上,且BE:EC=2:1,∠EAF=30°,则CF:FD=$\frac{1+13\sqrt{3}}{23}$.
分析 延长AF,与BC的延长线交于点G. 由已知条件BE:EC=2:1,得到BE:BC=2:3,即BE:AB=2:3 根据三角函数的定义得到tan∠BAE=$\frac{2}{3}$,tan∠GAE=tan30°=$\frac{\sqrt{3}}{3}$,于是得到tan∠GAB=tan(∠BAE+∠GAE)=$\frac{tan∠BAE+tan∠GAE}{1-tan∠BAE•tan∠GAE}$=$\frac{24+13\sqrt{3}}{23}$,证得BG:AB=$\frac{24+13\sqrt{3}}{23}$,于是得到结论.
解答 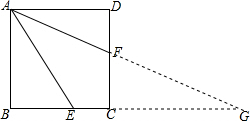 解:延长AF,与BC的延长线交于点G.
解:延长AF,与BC的延长线交于点G.
∵BE:EC=2:1,
∴BE:BC=2:3,即BE:AB=2:3
∴tan∠BAE=$\frac{2}{3}$,tan∠GAE=tan30°=$\frac{\sqrt{3}}{3}$,
∴tan∠GAB=tan(∠BAE+∠GAE)
=$\frac{tan∠BAE+tan∠GAE}{1-tan∠BAE•tan∠GAE}$
=$\frac{24+13\sqrt{3}}{23}$,
∴BG:AB=$\frac{24+13\sqrt{3}}{23}$,
∵AD∥CG,
∴△CGF∽△ADF,
∴$\frac{CF}{DF}=\frac{CG}{AD}$,
∵AD=BC,
∴$\frac{CF}{DF}$=$\frac{CG}{BC}$=$\frac{BG-BC}{BC}$=$\frac{BG}{BC}$-1=$\frac{BG}{AB}$-1=$\frac{24+13\sqrt{3}}{23}$-1=$\frac{1+13\sqrt{3}}{23}$.
故答案为:$\frac{1+13\sqrt{3}}{23}$.
点评 本题考查了相似三角形的判定和性质,锐角三角函数,两角和的正切值,正方形的性质,正确的作出辅助线是解题的关键.

| A. | 2 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4 |
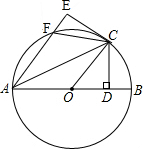 如图,AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于D.△ACD沿AC翻折后点D落在点E,AE交⊙O于点F;连接OC、FC.
如图,AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于D.△ACD沿AC翻折后点D落在点E,AE交⊙O于点F;连接OC、FC.