题目内容
16.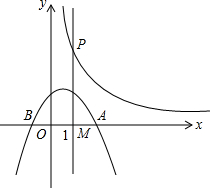 如图,抛物线L:y=-$\frac{1}{2}$(x-t)(x-t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=12.
如图,抛物线L:y=-$\frac{1}{2}$(x-t)(x-t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=12.(1)求k的值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标.
分析 (1)设P(x,y),则可表示出MP,由M为OA的中点,可求得OA,由条件可求得xy,则可求得k的值;
(2)把t=1,代入抛物线解析式,令y=0可求得A、B两点的坐标,可求得AB的长,再求得抛物线的对称轴和直线MP的方程,可求得直线MP与对称轴之间的距离;
(3)可用t表示出A、B两点的坐标,进一步可表示出直线MP的解析式,再根据顶点的位置可求得其最大值,可表示出G的坐标.
解答 解:
(1)设P(x,y)则MP=y,
∵M为OA的中点,
∴OA=2x,
∵OA•MP=12,
∴2xy=12,
∴xy=6,
∴k=6;
(2)当t=1,y=0时,0=-$\frac{1}{2}$(x-1)(x-1+4),解得x=1或x=-3,
∴A(1,0)、B(-3,0),
∴AB=4;
∴抛物线L的对称轴为直线x=$\frac{1+(-3)}{2}$=-1,
∵OA=1,
∴MP为直线x=$\frac{1}{2}$,
∴直线MP与L对称轴之间的距离为$\frac{3}{2}$;
(3)在y=-$\frac{1}{2}$(x-t)(x-t+4)中,令y=0可得-$\frac{1}{2}$(x-t)(x-t+4)=0,解得x=t或x=t-4,
∴A(t,0),B(t-4,0),
∴抛物线L的对称轴为直线x=$\frac{t+t-4}{2}$=t-2,
又∵MP为直线x=$\frac{t}{2}$,
∴当抛物线L的顶点在直线MP上或左侧时,即t-2≤$\frac{t}{2}$时,解得t≤4,此时,顶点(t-2,2)为图象G最高点的坐标;
当抛物线L的顶点在直线MP右侧时,即t-2>$\frac{t}{2}$时,解得t>4,此时时,交点直线MP与抛物线L的交点为($\frac{t}{2}$,-$\frac{1}{8}$t2+t),为图象G最高点的坐标.
点评 本题为二次函数和反比例函数的综合应用,涉及二次函数的性质、一元二次方程、分类讨论思想和方程思想等知识.在(1)中注意方程思想的应用,在(2)中求得A、B的坐标是解题的关键,在(3)中注意分两种情况.本题考查知识点较多,综合性较强,难度适中.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案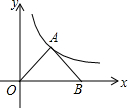 已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.
已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.
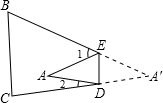 如图所示,把纸片△A′BC沿DE折叠,点A′落在四边形BCDE内部点A处.
如图所示,把纸片△A′BC沿DE折叠,点A′落在四边形BCDE内部点A处.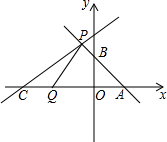 如图,直线l1:y1=-x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2=$\frac{1}{2}$x+b过点P,与x轴交于点C.
如图,直线l1:y1=-x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2=$\frac{1}{2}$x+b过点P,与x轴交于点C. 如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.
如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.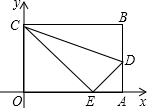 如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处.
如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处.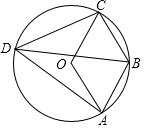 如图,四边形ABCD为⊙O的内接四边形,若四边形ABCO为平行四边形,则∠ADB=30°.
如图,四边形ABCD为⊙O的内接四边形,若四边形ABCO为平行四边形,则∠ADB=30°.