题目内容
8.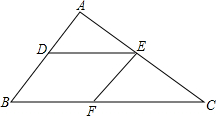 如图,在△ABC中,D、E、F分别是AB、AC、BC上的点,且DE∥BC,EF∥AB,AE:EC=3:4,BC=21,求BF的长.
如图,在△ABC中,D、E、F分别是AB、AC、BC上的点,且DE∥BC,EF∥AB,AE:EC=3:4,BC=21,求BF的长.
分析 先由DE∥BC,EF∥AB得出四边形BDEF是平行四边形,那么BF=DE.再由AE:EC=3:4,得出AE:AC=3:7.由DE∥BC,根据平行线分线段成比例定理得出DE:BC=AE:AC=3:7,将BC=21代入求出DE的长,即为BF的长.
解答 解:∵DE∥BC,EF∥AB,
∴四边形BDEF是平行四边形,
∴BF=DE.
∵AE:EC=3:4,
∴AE:AC=3:7.
∵DE∥BC,
∴DE:BC=AE:AC=3:7,即DE:21=3:7,
∴DE=9,
∴BF=9.
点评 此题考查了平行线分线段成比例定理,平行四边形的判定与性质,比例的性质,难度不大,得出BF=DE,从而利用转化思想是解题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 如图所示,点C是线段AB的黄金分割点,AC>BC,D、E分别是AC、BC的中点,仔细观察,试说明点DE黄金分割点.
如图所示,点C是线段AB的黄金分割点,AC>BC,D、E分别是AC、BC的中点,仔细观察,试说明点DE黄金分割点.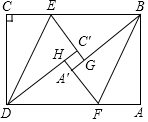 将一张矩形ABCD纸片,按如图进行折叠,分别在BC,AD两边上取两点E,F,使CE=AF,分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C′DE′与△A′BF,且边EC′的延长线与A′B交于点G,边FA的延长线与C′D交于一点H,已知tan∠EBG=$\frac{3}{4}$,A′G=6,C′G=4,则线段BC=52.
将一张矩形ABCD纸片,按如图进行折叠,分别在BC,AD两边上取两点E,F,使CE=AF,分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C′DE′与△A′BF,且边EC′的延长线与A′B交于点G,边FA的延长线与C′D交于一点H,已知tan∠EBG=$\frac{3}{4}$,A′G=6,C′G=4,则线段BC=52.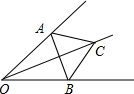 如图所示,OA=OB,AC=BC,求证:OC⊥AB.
如图所示,OA=OB,AC=BC,求证:OC⊥AB. 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上的一点,点E在BC边上,连接AE、DE、DC,AE=CD.求证:∠BAE=∠BCD.
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上的一点,点E在BC边上,连接AE、DE、DC,AE=CD.求证:∠BAE=∠BCD.