题目内容
7.如图,△ABC的三个顶点和它内部的点P1,把△ABC分成3个互不重叠的小三角形;△ABC的三个顶点和它内部的点P1、P2,把△ABC分成5个互不重叠的小三角形;△ABC的三个顶点和它内部的点 P1、P2、P3,把△ABC分成7个互不重叠的小三角形;…△ABC的三个顶点和它内部的点 P1、P2、P3、…、Pn,把△ABC分成2n+1个互不重叠的小三角形.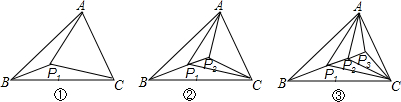
分析 利用图形得到,△ABC的三个顶点和它内部的点P1,把△ABC分成互不重叠的小三角形的个数=3+2×0;△ABC的三个顶点和它内部的点P1、P2,把△ABC分成互不重叠的小三角形的个数=3+2×1;△ABC的三个顶点和它内部的点 P1、P2、P3,把△ABC分成互不重叠的小三角形的个数=3+2×2,即分成的互不重叠的小三角形的个数为3加上P点的个数与1的差的2倍,从而得到△ABC的三个顶点和它内部的点 P1、P2、P3、…、Pn,把△ABC分成的互不重叠的小三角形的个数.
解答 解:如图,△ABC的三个顶点和它内部的点P1,把△ABC分成的互不重叠的小三角形的个数=3+2×0,
△ABC的三个顶点和它内部的点P1、P2,把△ABC分成的互不重叠的小三角形的个数=3+2×1,
△ABC的三个顶点和它内部的点 P1、P2、P3,把△ABC分成的互不重叠的小三角形的个数=3+2×2,
所以△ABC的三个顶点和它内部的点 P1、P2、P3、…、Pn,把△ABC分成的互不重叠的小三角形的个数=3+2(n-1).
故答案为:2n+1.
点评 本题考查了规律型:图形的变化类:对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,然后通过分析找到各部分的变化规律后直接利用规律求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.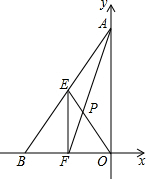 如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P的坐标为( )
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P的坐标为( )
 如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P的坐标为( )
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P的坐标为( )| A. | (-1,$\frac{4}{3}$) | B. | (-$\frac{3}{2}$,2) | C. | (-$\frac{3}{2}$,$\frac{4}{3}$) | D. | (-1,2) |
19.某中学开展“阳光体育一小时”活动,根据学校实际情况,如图决定开设“A:踢毽子,B:篮球,C:跳绳,D:乒乓球”四项运动项目(每位同学必须选择一项),为了解学生最喜欢哪一项运动项目,随机抽取了一部分学生进行调查,丙将调查结果绘制成如图的统计图,则参加调查的学生中最喜欢跳绳运动项目的学生数为( )
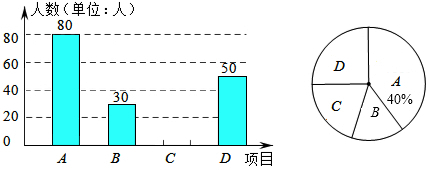

| A. | 240 | B. | 120 | C. | 80 | D. | 40 |
16.不等式组$\left\{\begin{array}{l}{2x+1≤5}\\{x+2>1}\end{array}\right.$的解集是( )
| A. | -1<x<2 | B. | 1<x≤2 | C. | -1<x≤2 | D. | -1<x≤3 |
17.下列四个实数中最大的是( )
| A. | -5 | B. | 0 | C. | π | D. | 3 |
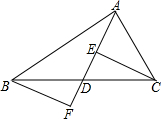 如图:在△ABC中,点D为BC边上的中点,连接AD,点E为线段AD上的一点,连接CE,过点B作BF∥CE交AD的延长线于点F,求证:CE=BF.
如图:在△ABC中,点D为BC边上的中点,连接AD,点E为线段AD上的一点,连接CE,过点B作BF∥CE交AD的延长线于点F,求证:CE=BF.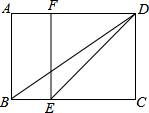 已知:如图,在矩形ABCD中,E是BC边上一点,DE平分∠ADC,EF∥DC交AD边于点F,连结BD.
已知:如图,在矩形ABCD中,E是BC边上一点,DE平分∠ADC,EF∥DC交AD边于点F,连结BD. 正方形A1B1C1O和A2B2C2C1按如图所示方式放置,点A1,A2在直线y=x+1上,点C1,C2在x轴上.已知A1点的坐标是(0,1),则点B2的坐标为(3,2).
正方形A1B1C1O和A2B2C2C1按如图所示方式放置,点A1,A2在直线y=x+1上,点C1,C2在x轴上.已知A1点的坐标是(0,1),则点B2的坐标为(3,2).