题目内容
 ∠BOC=60°,OE平分∠AOC,OF平分∠BOC,若AO⊥BO,则∠EOF是多少度?
∠BOC=60°,OE平分∠AOC,OF平分∠BOC,若AO⊥BO,则∠EOF是多少度?考点:垂线,角平分线的定义
专题:
分析:根据垂线的定义,可得∠AOB的度数,根据角的和差,可得∠AOC的度数,根据角平分线的性质,可得∠COE、∠COF的度数,根据角的和差,可得答案.
解答:解:由AO⊥BO,得∠AOB=90°,
由角的和差,得∠AOC=∠AOB+∠BOC=150°.
由OE平分∠AOC,OF平分∠BOC,得∠COE=
∠AOC=
×150°=75°,∠COF=
∠BOC=
×60°=30°.
由角的和差,得∠EOF=∠COE-∠COF=75°-30°=45°.
由角的和差,得∠AOC=∠AOB+∠BOC=150°.
由OE平分∠AOC,OF平分∠BOC,得∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由角的和差,得∠EOF=∠COE-∠COF=75°-30°=45°.
点评:本题考查了垂线,利用了垂线的定义,角平分线的定义,角的和差.

练习册系列答案
相关题目
下列一元二次方程没有实数根的是( )
| A、x2=x |
| B、x2-9=0 |
| C、x2-2x-8=0 |
| D、x2-x+3=0 |
 如图,长方形的长为10cm,宽为6cm,四角割去边长为xcm的小正方形折叠后形成一个无盖长方体,这个长方体的长是
如图,长方形的长为10cm,宽为6cm,四角割去边长为xcm的小正方形折叠后形成一个无盖长方体,这个长方体的长是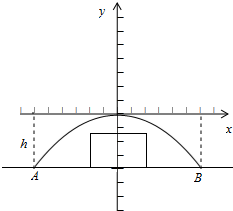 如图所示,有一抛物线形涵洞,其函数表达式为y=ax2(a≠0).涵洞跨度AB=12m,内部高度h=4m.为了安全,卡车经过涵洞时,载货(矩形)最高处与其正上方顶部之间的距离不能小于0.5m.现有一辆运货卡车欲通过涵洞,经测量该车宽4m,载货最高处距地面2.5m.问该车能否通过,为什么?
如图所示,有一抛物线形涵洞,其函数表达式为y=ax2(a≠0).涵洞跨度AB=12m,内部高度h=4m.为了安全,卡车经过涵洞时,载货(矩形)最高处与其正上方顶部之间的距离不能小于0.5m.现有一辆运货卡车欲通过涵洞,经测量该车宽4m,载货最高处距地面2.5m.问该车能否通过,为什么? 如图是某宾馆大厅到二楼的楼梯设计图(图中每个小正方形的边长为1个单位长度),中间为平台DE,DM、EN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N.设计师建立了相应的坐标系,测量后部分点的坐标如下表:
如图是某宾馆大厅到二楼的楼梯设计图(图中每个小正方形的边长为1个单位长度),中间为平台DE,DM、EN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N.设计师建立了相应的坐标系,测量后部分点的坐标如下表:
 如图所示,试说出图中的同位角、内错角及同旁内角分别有几组?
如图所示,试说出图中的同位角、内错角及同旁内角分别有几组?