题目内容
9. 若x满足(9-x)(x-4)=4,求(4-x)2+(x-9)2的值.
若x满足(9-x)(x-4)=4,求(4-x)2+(x-9)2的值.解:设9-x=a,x-4=b,则(9-x)(x-4)=ab=4,a+b=(9-x)+(x-4)=5,
∴(9-x)2+(x-4)2=a2+b2=(a+b)2-2ab=52-2×4=13
请仿照上面的方法求解下面问题:
(1)若x满足(5-x)(x-2)=2,求(5-x)2+(x-2)2的值
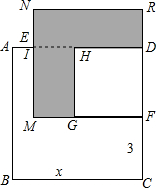
(2)已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是48,分别以MF、DF作正方形,求阴影部分的面积.
分析 (1)设(5-x)=a,(x-2)=b,根据已知等式确定出所求即可;
(2)设正方形ABCD边长为x,进而表示出MF与DF,求出阴影部分面积即可.
解答  解:(1)设(5-x)=a,(x-2)=b,则(5-x)(x-2)=ab=2,a+b=(5-x)+(x-2)=3,
解:(1)设(5-x)=a,(x-2)=b,则(5-x)(x-2)=ab=2,a+b=(5-x)+(x-2)=3,
∴(5-x)2+(x-2)2=(a+b)2-2ab=32-2×2=5;
(2)∵正方形ABCD的边长为x,AE=1,CF=3,
∴MF=DE=x-1,DF=x-3,
∴(x-1)•(x-3)=48,
∴(x-1)-(x-3)=2,
∴阴影部分的面积=FM2-DF2=(x-1)2-(x-3)2.
设(x-1)=a,(x-3)=b,则(x-1)(x-3)=ab=48,a-b=(x-1)-(x-3)=2,
∴(x-1)2-(x-3)2=a2-b2=(a+b)(a-b)=14×2=28.即阴影部分的面积是28.
点评 本题考查了完全平方公式的几何背景.应从整体和部分两方面来理解完全平方公式的几何意义;主要围绕图形面积展开分析.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列剪纸作品中,是中心对称图形的为( )
| A. |  | B. |  | C. |  | D. |  |
18.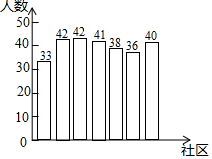 小楠所在社会实践活动小组的同学们响应“垃圾分类,从我做起”的号召,主动到附近的7个社区宣传垃圾分类.她们记录的各社区参加活动的人数如图所示,那么这组数据的众数和中位数分别是( )
小楠所在社会实践活动小组的同学们响应“垃圾分类,从我做起”的号召,主动到附近的7个社区宣传垃圾分类.她们记录的各社区参加活动的人数如图所示,那么这组数据的众数和中位数分别是( )
 小楠所在社会实践活动小组的同学们响应“垃圾分类,从我做起”的号召,主动到附近的7个社区宣传垃圾分类.她们记录的各社区参加活动的人数如图所示,那么这组数据的众数和中位数分别是( )
小楠所在社会实践活动小组的同学们响应“垃圾分类,从我做起”的号召,主动到附近的7个社区宣传垃圾分类.她们记录的各社区参加活动的人数如图所示,那么这组数据的众数和中位数分别是( )| A. | 42,40 | B. | 42,38 | C. | 2,40 | D. | 2,38 |
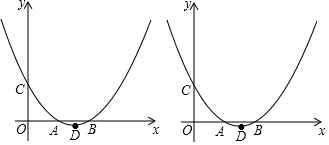
 如图,已知sin∠AOB=0.1,OC=1.2厘米,则小矩形木条的厚度CD=0.12厘米.
如图,已知sin∠AOB=0.1,OC=1.2厘米,则小矩形木条的厚度CD=0.12厘米.