题目内容
18．用适当的方法解下列方程：（1）（x+1）（x-2）=x-2
（2）（2x+1）2=x2+2．
分析 （1）先把方程变形为（x+1）（x-2）-（x-2）=0，然后利用因式分解法解方程；
（2）先把方程化为一般式，然后利用求根公式法解方程．
解答 解：（1）（x+1）（x-2）-（x-2）=0，
（x-2）（x+1-1）=0，
x-2=0或x+1-1=0，
所以x1=2，x2=0；
（2）3x2+4x-1=0，
△=42-4×3×（-1）=28，
x=$\frac{-4±2\sqrt{7}}{2×3}$=$\frac{-2±\sqrt{7}}{3}$
所以x1=$\frac{-2+\sqrt{7}}{3}$，x2=$\frac{-2-\sqrt{7}}{3}$．
点评 本题考查了解一元二次方程-因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．也考查了公式法解一元二次方程．
练习册系列答案
相关题目
6．下列各组数中，不是二元一次方程x+y=10的一组解的是（ ）
| A． | $\left\{{\begin{array}{l}{x=-3}\\{y=13}\end{array}}\right.$ | B． | $\left\{{\begin{array}{l}{x=12}\\{y=-2}\end{array}}\right.$ | C． | $\left\{{\begin{array}{l}{x=2}\\{y=5}\end{array}}\right.$ | D． | $\left\{{\begin{array}{l}{x=4}\\{y=6}\end{array}}\right.$ |
若x满足（9-x）（x-4）=4，求（4-x）2+（x-9）2的值．
3．小英把1000元钱按年利率2.45%存入银行，存期为两年，那么计算到期时她可以从银行取回多少钱（不计利息税），列式正确的是（ ）
| A． | 1000×2.45%×2 | B． | （1000×2.45%+1000）×2 | ||
| C． | 1000×2.45%+1000 | D． | 1000×2.45%×2+1000 |
10．下列根式中，属于最简二次根式的是（ ）
| A． | $\sqrt{17}$ | B． | $\sqrt{12}$ | C． | $\sqrt{2.4}$ | D． | $\sqrt{\frac{1}{3}}$ |
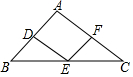如图，△ABC的边AB、BC、CA的中点分别是D、E、F，已知AB=8，AC=10，则四边形ADEF的周长是（ ）
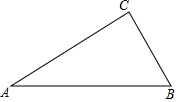如图，在△ABC中，AC＞BC．