题目内容
14．在△ABC中，AB=AC=10，BC=16，则tanB=$\frac{3}{4}$．分析 根据题意画出图形，由等腰三角形的性质求出BD的长，根据勾股定理求出AD的长，再根据锐角三角函数的定义即可求出tanB的值．
解答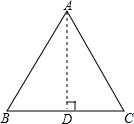 
解：如图，等腰△ABC中，AB=AC=10，BC=16，
过A作AD⊥BC于D，则BD=8，
在Rt△ABD中，AB=10，BD=8，则
AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6，
故tanB=$\frac{AD}{BD}$=$\frac{6}{8}$=$\frac{3}{4}$．
故答案为：$\frac{3}{4}$．
点评 本题考查了解直角三角形，等腰三角形的性质，正确作出辅助线，构造直角三角形是解题的关键．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
5．下列运算中，正确的是（ ）
| A． | $\sqrt{9}=±3$ | B． | （a2）3=a6 | C． | 3a•2a=6a | D． | 3-2=-6 |
（1）已知点A（m+1，2n-3）关于原点对称的点A1（2m+1，-n-1），求m、n的值．
19．在下列四组点中，可以在同一个正比例函数图象上的一组点是（ ）
| A． | （-2，-3），（4，-6） | B． | （-2，3），（4，6） | C． | （2，-3），（-4，6） | D． | （2，3），（-4，6） |