题目内容
20.阅读理解.若方程x2+px+q=0的根为x1=a、x2=b,则a+b=-p、ab=q,所以x2+px+q=x2-(a+b)x+ab=(x-a)(x-b),也就是说如果知道x2+px+q=0的两根就可以对x2+px+q分解因式了.例如在实数范围内分解x2-x-1
解:设x2-x-1=0解得x=$\frac{1±\sqrt{5}}{2}$则x2-x-1=(x-$\frac{1+\sqrt{5}}{2}$)(x-$\frac{1-\sqrt{5}}{2}$)
(1)在实数范围内分解二次三项式:y2-3y-2
(2)试分解2x2+x-4
(3)探索:二次三项式ax2+bx+c(a≠0、a、b、c是常数)满足什么条件时,在实数范围内可分解因式,满足什么条件时,不能在实数范围内分解因式.
分析 (1)直接解方程y2-3y-2=0,进而分解因式即可;
(2)直接解方程2x2+x-4=0,进而分解因式即可;
(3)由(1)(2)可得ax2+bx+c=0方程有实数根是才能分解因式,进而得出答案.
解答 解:(1)设y2-3y-2=0
解得:y=$\frac{3±\sqrt{17}}{2}$,
则y2-3y-2=(x-$\frac{3+\sqrt{17}}{2}$)(y-$\frac{3-\sqrt{17}}{2}$);
(2)设2x2+x-4=0
解得:y=$\frac{-1±\sqrt{33}}{4}$,
则2x2+x-4=(x-$\frac{-1+\sqrt{33}}{4}$)(x-$\frac{-1-\sqrt{33}}{4}$);
(3)二次三项式ax2+bx+c(a≠0、a、b、c是常数)满足b2-4ac≥0条件时,在实数范围内可分解因式,
满足b2-4ac<0时,不能在实数范围内分解因式.
点评 此题主要考查了因式分解以及一元二次方程的解法,正确解方程是解题关键.

练习册系列答案
相关题目
11.下列图形中,对称轴数量最多的是( )
| A. |  | B. |  | C. |  | D. |  |
15.在估算一元二次方程x2+12x-15=0的根时,小彬列表如下:
由此可估算方程x2+12x-15=0的一个根x的范围是1.1<x<1.2.
| x | 1 | 1.1 | 1.2 | 1.3 |
| x2+12x-15 | -2 | -0.59 | 0.84 | 2.29 |
9.有一组数(1),(3,5),(7,9,11),…2017也在某一个括号当中,它是这个括号内从左边数的( )
| A. | 第17个数 | B. | 第18个数 | C. | 第19个数 | D. | 第20个数 |

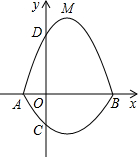 如图所示,在平面直角坐标系中,A、B为x轴上两点,C、D为y轴上两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.
如图所示,在平面直角坐标系中,A、B为x轴上两点,C、D为y轴上两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.