题目内容
3.解不等式组$\left\{\begin{array}{l}11-2({x-3})≥3({x-1})\\ x+2>\frac{1-2x}{3}\end{array}\right.$,并求它的整数解.分析 先求出两个不等式的解集,再求其公共解.
解答 解:$\left\{\begin{array}{l}{11-2(x-3)≥3(x-1)①}\\{x+2>\frac{1-2x}{3}②}\end{array}\right.$
由①得,x≤4,
由②得,x>-1,
不等式组的解集为:-1<x≤4,
所以其整数解为:0,1,2,3,4.
点评 本题主要考查不等式组的解法,及根据未知数的范围确定它所满足的特殊条件的值.一般方法是先解不等式组,再根据解集求出特殊值;不等式组的解集,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
11.一个DNA分子的直径约为0.0000002cm,用科学记数法表示为( )
| A. | 0.2×10-6cm | B. | 2×10-6cm | C. | 0.2×10-7cm | D. | 2×10-7cm |
8.一个多边形的每一个外角都是72°,那么这个多边形的内角和为( )
| A. | 540° | B. | 720° | C. | 900° | D. | 1080° |
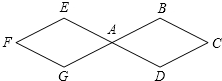 如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始AGFEADCBAG…的顺序沿菱形的边循环爬行,当电子甲虫爬行1945cm时停下,则它停的位置是点G.
如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始AGFEADCBAG…的顺序沿菱形的边循环爬行,当电子甲虫爬行1945cm时停下,则它停的位置是点G.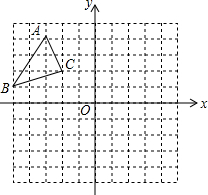 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(-3,4).
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(-3,4).