题目内容
11. 如图,抛物线与x轴相交于B、C两点,与y轴相交于点A,P(a,-a2+$\frac{7}{2}$a+m)(a为任意实数)在抛物线上,直线y=kx+b经过A、B两点,平行于y轴的直线x=2交AB于点D,交抛物线于点E.
如图,抛物线与x轴相交于B、C两点,与y轴相交于点A,P(a,-a2+$\frac{7}{2}$a+m)(a为任意实数)在抛物线上,直线y=kx+b经过A、B两点,平行于y轴的直线x=2交AB于点D,交抛物线于点E.(1)当代数式-a2+$\frac{7}{2}$a+m的值随a的增大而减小时,求a的取值范围.
(2)当m=2时,直线x=t(0≤t≤4)交AB于点F,交抛物线于点G.若FG:DE=1:2,求t值.
(3)连结EO,当EO平分∠AED时,求m的值.
分析 (1)根据二次函数的性质,可得答案;
(2)根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得DE,FG的长,根据比例FG:DE=1:2,可得关于t的方程,根据解方程,可得答案;
(3)根据平行线的性质,可得∠2=∠3,根据等腰三角形的判定,可得关于m的方程,根据解方程,可得答案.
解答 解:(1)y=-a2+$\frac{7}{2}$a+m,
对称轴a=-$\frac{\frac{7}{2}}{-2}$=$\frac{7}{4}$,
-1<0,开口向下所以a≥$\frac{7}{4}$时,代数式-a2+$\frac{7}{2}$a+m的值随a的增大而减小;
(2)m=2时,抛物线:y=-x2+$\frac{7}{2}$x+2,
当x=0时,y=2,即A(0,2),当y=0时,x=4,x=-$\frac{1}{2}$,即B(4,0),
将A、B点坐标代入函数解析式,得
直线AB:y=-$\frac{1}{2}$x+2,
当x=2时,y=-22+$\frac{7}{2}$×2+2=5,即E(2,5),当x=2时,y=-$\frac{1}{2}$×2+2=1,即D(2,1),
DE=4.
当x=t时,y=-t2+$\frac{7}{2}$×t+2,即E(2,-t2+$\frac{7}{2}$×t+2),当x=t时,y=-$\frac{1}{2}$×t+2,即D(2,1),
FG═-t2+$\frac{7}{2}$×t+2(-$\frac{1}{2}$t+2)=-t2+4t.
若FG:DE=1:2,则t2-4t+2=0,
所以t=2±$\sqrt{2}$,满足0≤t≤4,
∴FG:DE=1:2,t的值为2$±\sqrt{2}$;
(3)如图 ,
,
OA=m.
当x=2时,y═-22+$\frac{7}{2}$×2+m=3+m,
E(2,3+m).
当EO平分∠AED时,∠1=∠2,
∵AO∥DE,
∴∠2=∠3,
∴∠1=∠3,
∴OA=AE,
m2=22+(3+m-m)2,
解得m=$\sqrt{13}$.
点评 本题考查了二次函数综合题,利用二次函数的性质是阶梯关键;利用平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标得出DE,FG的长是解题关键;利用等腰三角形的判定的出关于m的方程是解题关键.

 如图,在扇形AOB中,∠AOB=90°,半径OA=6,将扇形AOB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,则整个阴影部分的面积为( )
如图,在扇形AOB中,∠AOB=90°,半径OA=6,将扇形AOB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,则整个阴影部分的面积为( )| A. | 9π-9 | B. | 9π-6$\sqrt{3}$ | C. | 9π-18 | D. | 9π-12$\sqrt{3}$ |
| A. | x=-2 | B. | x=2 | C. | x=1 | D. | x=1 或 x=2 |
 如图,直线a、b被直线c所截,a∥b,∠1=∠2,若∠4=65°,则∠3等于( )
如图,直线a、b被直线c所截,a∥b,∠1=∠2,若∠4=65°,则∠3等于( )| A. | 30° | B. | 50° | C. | 65° | D. | 115° |
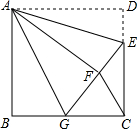 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①CE=4;②△ABG≌△AFG;③BG=GC;④AG∥CF.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①CE=4;②△ABG≌△AFG;③BG=GC;④AG∥CF.其中正确结论的个数是( ) 已知函数y=$\frac{6}{x}$-1与函数y=kx交于点A(2,b)、B(-3,m)两点(点A在第一象限),
已知函数y=$\frac{6}{x}$-1与函数y=kx交于点A(2,b)、B(-3,m)两点(点A在第一象限),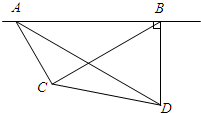 如图,在我市的上空一架飞机由A向B沿水平直线方向飞行,沿航线AB的正下方有两个景点水城明珠大剧院(记为点C),光岳楼(记为点D),飞机在A处时,测得景点C、D在飞机的前方,俯角分别为60°和30°.飞机飞行了3千米到B处时,往后测得景点C的俯角为30°.而景点D恰好在飞机的正下方,求水城明珠大剧院与光岳楼之间的距离(最后结果精确到0.1千米)
如图,在我市的上空一架飞机由A向B沿水平直线方向飞行,沿航线AB的正下方有两个景点水城明珠大剧院(记为点C),光岳楼(记为点D),飞机在A处时,测得景点C、D在飞机的前方,俯角分别为60°和30°.飞机飞行了3千米到B处时,往后测得景点C的俯角为30°.而景点D恰好在飞机的正下方,求水城明珠大剧院与光岳楼之间的距离(最后结果精确到0.1千米)