Question

19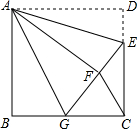．如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．下列结论：①CE=4；②△ABG≌△AFG；③BG=GC；④AG∥CF．其中正确结论的个数是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 在直角△ECG中，根据勾股定理可证BG=GC；根据翻折变换的性质和正方形的性质可证Rt△ABG≌Rt△AFG；通过证明∠AGB=∠AGF=∠GFC=∠GCF，由平行线的判定可得AG∥CF即可．

解答 解：①正确，
理由：
∵正方形ABCD中，AB=6，点E在边CD上，且CD=3DE，
∴CE=4，
②正确．
理由：
∵AB=AD=AF，AG=AG，∠B=∠AFG=90°，
∴Rt△ABG≌Rt△AFG（HL）；
③正确．
理由：
EF=DE=$\frac{1}{3}$CD=2，设BG=FG=x，则CG=6-x．
在直角△ECG中，根据勾股定理，得（6-x）²+4²=（x+2）²，
解得x=3．
∴BG=3=6-3=GC；
④正确．
理由：
∵CG=BG，BG=GF，
∴CG=GF，
∴△FGC是等腰三角形，∠GFC=∠GCF．
又∵Rt△ABG≌Rt△AFG；
∴∠AGB=∠AGF，∠AGB+∠AGF=2∠AGB=180°-∠FGC=∠GFC+∠GCF=2∠GFC=2∠GCF，
∴∠AGB=∠AGF=∠GFC=∠GCF，
∴AG∥CF；
∴正确的个数有①②③④．
故选D

点评 本题考查的是翻折变换的性质和正方形的性质，全等三角形的判定与性质，勾股定理，平行线的判定，有一定的难度．