��Ŀ����
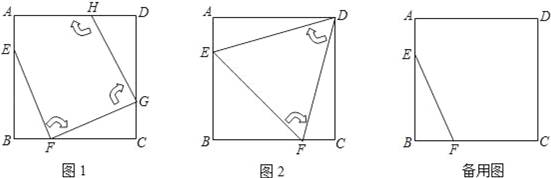
��ͼ1���߳�Ϊ4��������ABCD�У���E��AB���ϣ������A��B�غϣ�����F��BC���ϣ������B��C�غϣ���
��һ�β��������߶�EF�Ƶ�F˳ʱ����ת������E������������ʱ����Ϊ��G��
�ڶ��β��������߶�FG�Ƶ�G˳ʱ����ת������F������������ʱ����Ϊ��H��
���˲�����ȥ��
��1��ͼ2�еġ�EFD�Ǿ������β�����õ��ģ�����״Ϊ�����������������ʱ�߶�EF�ij���
��2�����������β����ɵõ��ı���EFGH��
�����ж��ı���EFGH����״Ϊ����������������ʱAE��BF��������ϵ����������������
���Ԣ��еĽ���Ϊǰ�ᣬ��AE�ij�Ϊx���ı���EFGH�����Ϊy����y��x�ĺ�����ϵʽ�����y��ȡֵ��Χ��

��
�����㡿���α任�ۺ��⣮
����������1������ת���ʣ��á�EFD�ǵȱ������Σ����õȱ������ε����ʡ����ɶ������EF�ij���
��2�����ı���EFGH���ı߳�����ȣ������������Σ�����������ȫ��֤��AE=BF��
�������y�ı���ʽ������һ�����κ��������ö��κ������������ֵ��y��ȡֵ��Χ��
����𡿽⣺��1������ͼ2������ת���ʿ�֪EF=DF=DE�����DEFΪ�ȱ������Σ�
��Rt��ADE��Rt��CDF��


��Rt��ADE��Rt��CDF��HL��
��AE=CF��
��AE=CF=x����BE=BF=4��x
���BEFΪ����ֱ�������Σ�
��EF=
 BF=
BF=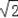
 ��4��x����
��4��x����
��DE=DF=EF=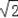
 ��4��x����
��4��x����
��Rt��ADE�У��ɹ��ɶ����ã�AE2+AD2=DE2������x2+42=[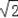
 ��4��x��]2��
��4��x��]2��
��ã�x1=8��4
 ��x2=8+4
��x2=8+4
 ����ȥ��
����ȥ��
��EF=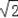
 ��4��x��=4
��4��x��=4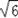
 ��4
��4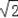
 ��
��
DEF����״Ϊ�ȱ������Σ�EF�ij�Ϊ4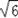
 ��4
��4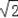
 ��
��
��2�����ı���EFGH����״Ϊ�����Σ���ʱAE=BF���������£�
�����⻭��ͼ�Σ����ͼ1��ʾ��


����ת���ʿ�֪��EF=FG=GH=HE����EFG=90�㣬���ı���EFGH����״Ϊ�����Σ�
�ߡ�1+��2=90�㣬��2+��3=90�㣬
���1=��3��
�ߡ�3+��4=90�㣬��2+��3=90�㣬
���2=��4��
�ڡ�AEH���BFE�У�
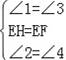

���AEH�ա�BFE��ASA��
��AE=BF��
�����â��н��ۣ���֤��AEH����BFE����CGF����DHG��Ϊȫ�������Σ�
��BF=CG=DH=AE=x��AH=BE=CF=DG=4��x��
��y=S������ABCD��4S��AEH=4��4��4��
 x��4��x��=2x2��8x+16��
x��4��x��=2x2��8x+16��
��y=2x2��8x+16��0��x��4��
��y=2x2��8x+16=2��x��2��2+8��
�൱x=2ʱ��yȡ����Сֵ8����x=0ʱ��y=16��
��y��ȡֵ��ΧΪ��8��y��16��
�������������Ǽ��α任�ۺ��⣬����ת�任Ϊ���������������Ρ�ȫ�������Ρ��ȱ������Ρ�����ֱ�������Ρ����ɶ��������κ�����֪ʶ�㣮�����ѶȲ������ض��ڼ��λ���֪ʶ�Ŀ��飬��һ�����⣮

 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д� �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д� ________��
________�� 

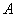 ��˫����
��˫����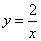 �ڵ�һ���ķ�֧�ϵ�һ�����㣬����
�ڵ�һ���ķ�֧�ϵ�һ�����㣬����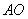 ���ӳ�����һ��֧�ڵ�
���ӳ�����һ��֧�ڵ�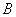 ������
������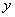 ��Ĵ��ߣ�����
��Ĵ��ߣ�����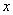 ��Ĵ��ߣ������߽��ڵ�
��Ĵ��ߣ������߽��ڵ�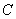 �����ŵ�
�����ŵ�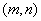 ����
����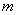 ��
��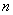 ����ı���ʽΪ( )
����ı���ʽΪ( ) B.
B.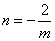 C.
C.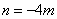 D.
D.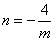
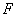 (N)������������ķ������ƶ��ľ���
(N)������������ķ������ƶ��ľ���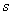 (m)֮��ɷ�����������ϵ����ͼ����ͼ��ʾ���ҵ�
(m)֮��ɷ�����������ϵ����ͼ����ͼ��ʾ���ҵ�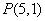 ����ͼ���ϣ������ﵽ10 Nʱ�����������ķ������ƶ��ľ����� m.
����ͼ���ϣ������ﵽ10 Nʱ�����������ķ������ƶ��ľ����� m.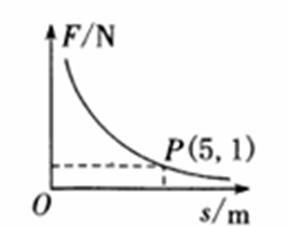
 ��
��
