题目内容
如图,E、F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE、BF交于点P.
(1)求证:CE=BF;
(2)求∠BPC的度数.
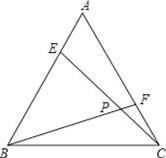

【考点】全等三角形的判定与性质;等边三角形的性质.
【分析】(1)欲证明CE=BF,只需证得△BCE≌△ABF;
(2)利用(1)中的全等三角形的性质得到∠BCE=∠ABF,则由图示知∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60°,即∠PBC+∠PCB=60°,所以根据三角形内角和定理求得∠BPC=120°.
【解答】(1)证明:如图,∵△ABC是等边三角形,
∴BC=AB,∠A=∠EBC=60°,
∴在△BCE与△ABF中,
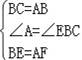
 ,
,
∴△BCE≌△ABF(SAS),
∴CE=BF;
(2)解:∵由(1)知△BCE≌△ABF,
∴∠BCE=∠ABF,
∴∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60°,即∠PBC+∠PCB=60°,
∴∠BPC=180°﹣60°=120°.
即:∠BPC=120°.
【点评】本题考查了全等三角形的判定与性质、等边三角形的性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

 阅读快车系列答案
阅读快车系列答案)如图①,小华设计了一个探究杠杆平衡条件的实验:在一根质地均匀的木杆中点 的左侧固定位置
的左侧固定位置 处悬挂重物
处悬挂重物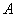 ,在中点
,在中点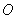 的右侧用一个弹簧秤向下拉,改变弹簧秤与点
的右侧用一个弹簧秤向下拉,改变弹簧秤与点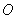 的距离
的距离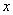 (cm),观察弹簧秤的示数
(cm),观察弹簧秤的示数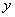 (N)的变化情况.实验数据记录如下表:
(N)的变化情况.实验数据记录如下表:
|
| … | 10 | 15 | 20 | 25 | 30 | … |
|
| … | 30 | 20 | 15 | 12 | 10 | … |
|
第24题
(1)把上表中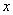 、
、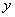 的各组对应值作为点的坐标,在平面直角坐标系中(如图②所示)描出相应的点,用平滑的曲线连接这些点并观察所得到的图像,猜测
的各组对应值作为点的坐标,在平面直角坐标系中(如图②所示)描出相应的点,用平滑的曲线连接这些点并观察所得到的图像,猜测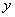 (N)与
(N)与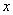 (cm)之间的函数关系,并求出函数表达式.
(cm)之间的函数关系,并求出函数表达式.
(2)当弹簧秤的示数为24N时,求弹簧秤与点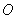 的距离.随着弹簧秤与点
的距离.随着弹簧秤与点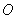 的距离不断减小,弹簧秤上的示数将发生怎样的变化?
的距离不断减小,弹簧秤上的示数将发生怎样的变化?

 的图像如图所示,对称轴为
的图像如图所示,对称轴为 ,若关于
,若关于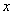 的一元二次方程
的一元二次方程 (
( 为实数)在
为实数)在 的范围
的范围



 上的两点,过点
上的两点,过点 轴,交
轴,交 于点
于点 ,垂足为
,垂足为 .若
.若 的面积为1,
的面积为1,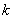 的值为 ( )
的值为 ( ) B.
B. C. 3 D. 4
C. 3 D. 4 
 = .
= .