题目内容
已知y1=x2-2x+1,y2=2x-k.
(1)当k=-1时,是否存在实数x,使得y1+y2=0?如果存在,请求出x的值,如果不存在,请说明理由.
(2)对给定的实数k,是否存在实数x,使y1=ky2?如果存在,请确定k的取值范围,如果不存在,请说明理由.
(1)当k=-1时,是否存在实数x,使得y1+y2=0?如果存在,请求出x的值,如果不存在,请说明理由.
(2)对给定的实数k,是否存在实数x,使y1=ky2?如果存在,请确定k的取值范围,如果不存在,请说明理由.
考点:根的判别式
专题:存在型
分析:(1)当k=-1时,由y1+y2=0得x2+2=0,根据判别式的意义得到方程没有实数解,则不存在实数x使y1+y2=0;
(2)由y1=ky2,则x2-2x+1=k(2x-k),整理得x2-(2+2k)+1+k2=0,再计算判别式的值得到△=8k,所以当k≥0时,方程有实数解,即对给定的实数k,存在实数x,使y1=ky2.
(2)由y1=ky2,则x2-2x+1=k(2x-k),整理得x2-(2+2k)+1+k2=0,再计算判别式的值得到△=8k,所以当k≥0时,方程有实数解,即对给定的实数k,存在实数x,使y1=ky2.
解答:解:(1)不存在.理由如下:
k=-1时,令y1+y2=0,得x2+2=0,
因为△=1-4×2<0,
所以方程没有实数解,
即不存在实数x使y1+y2=0;
(2)存在.
令y1=ky2,则x2-2x+1=k(2x-k),
整理得x2-(2+2k)+1+k2=0,
因为△=(2+2k)2-4(1+k2)=8k,
所以当k≥0时,方程有实数解,即对给定的实数k,存在实数x使y1=ky2.
k=-1时,令y1+y2=0,得x2+2=0,
因为△=1-4×2<0,
所以方程没有实数解,
即不存在实数x使y1+y2=0;
(2)存在.
令y1=ky2,则x2-2x+1=k(2x-k),
整理得x2-(2+2k)+1+k2=0,
因为△=(2+2k)2-4(1+k2)=8k,
所以当k≥0时,方程有实数解,即对给定的实数k,存在实数x使y1=ky2.
点评:本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
下列各组图形不一定相似的是( )
| A、两个等腰直角三角形 |
| B、各有一个角是150°的两个等腰三角形 |
| C、各有一个角是60°的两个直角三角形 |
| D、两个矩形 |
下列方程中,有实数根的是( )
| A、x2-x+1=0 |
| B、x2+2=0 |
| C、x2-x-2=0 |
| D、x2-3x+5=0 |
 如图是反比例函数y=
如图是反比例函数y=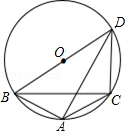 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则⊙O的半径为
如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则⊙O的半径为 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )