题目内容
若|m+2|+
=0,则多项式x2+y2-mxy-n分解的结果为 .
| n-4 |
考点:因式分解-分组分解法,非负数的性质:绝对值,非负数的性质:算术平方根
专题:
分析:首先利用绝对值以及非负数的性质得出m,n的值,进而利用分组分解法分解因式即可.
解答:解:∵|m+2|+
=0
∴m+2=0,n-4=0,
故m=-2,n=4,
故x2+y2-mxy-n
=x2+y2+2xy-4
=(x+y)2-4
=(x+y+2)(x+y-2).
故答案为:(x+y+2)(x+y-2).
| n-4 |
∴m+2=0,n-4=0,
故m=-2,n=4,
故x2+y2-mxy-n
=x2+y2+2xy-4
=(x+y)2-4
=(x+y+2)(x+y-2).
故答案为:(x+y+2)(x+y-2).
点评:此题主要考查了绝对值以及非负数的性质和分组分解法分解因式,得出m,n的值是解题关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知:甲乙两组数据的平均数都是5,甲组数据的方差S甲2=2.36,乙组数据的方差S乙2=9.67,下列结论中正确的是( )
| A、甲组数据的波动大 |
| B、乙组数据的波动大 |
| C、甲组数据与乙组数据的波动一样大 |
| D、甲组数据与乙组数据的波动不能比较 |
下列各式:-(-3);-|-3|;-32;(-3)4;
,计算结果为负数的有( )
| 3 | -27 |
| A、4个 | B、3个 | C、2个 | D、1个 |
如图,是小明画出的三角形各边上的高,其中最长边上的高的正确画法是( )
A、 |
B、 |
C、 |
D、 |
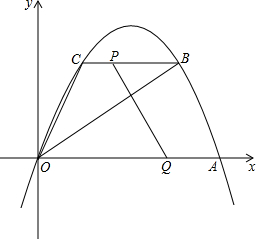 抛物线经过原点O(0,0),A(20,0),C(4,8),过C作平行于x轴的直线与抛物线另一交点为B,连OC,OB.
抛物线经过原点O(0,0),A(20,0),C(4,8),过C作平行于x轴的直线与抛物线另一交点为B,连OC,OB.