题目内容
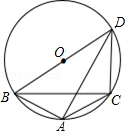如图，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为⊙O的直径，AD=6，则⊙O的半径为考点：圆周角定理,解直角三角形
专题：
分析：在△ABC中可求得∠BCA=30°，则∠BDA=30°，在Rt△ABD中可求得BD，从而可求得半径．
解答：解：∵AB=AC，∠BAC=120°，
∴∠BCA=30°，
又∵弧BA所对的圆周角为∠BDA和∠BCA，
∴∠BDA=30°，
在Rt△ABD中，AD=6，
可求得BD=4
，
∴⊙O的半径为2
，
故答案为：2
．
∴∠BCA=30°，
又∵弧BA所对的圆周角为∠BDA和∠BCA，
∴∠BDA=30°，
在Rt△ABD中，AD=6，
可求得BD=4
| 3 |
∴⊙O的半径为2
| 3 |
故答案为：2
| 3 |
点评：本题主要考查圆周角定理及等腰三角形的性质，利用条件求得∠BDA=30°是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
下列各式：-（-3）；-|-3|；-32；（-3）4；
，计算结果为负数的有（ ）
| 3 | -27 |
| A、4个 | B、3个 | C、2个 | D、1个 |
作一个角等于已知角用到下面选项的哪个基本事实（ ）
| A、SSS | B、SAS |
| C、ASA | D、AAS |
如图，是小明画出的三角形各边上的高，其中最长边上的高的正确画法是（ ）
A、 |
B、 |
C、 |
D、 |
在△ABC中，BC边不动，点A竖直向上运动，∠A越来越小，∠B和∠C越来越大，若∠A减小α度，∠B和∠C分别增加β度，γ度，则α，β，γ关系为（ ）
A、α=
| ||
B、β=
| ||
| C、α-β=γ | ||
| D、无法判定 |