题目内容
14.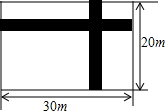 在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为多少?
在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为多少?解:设修建的路宽应为x米,余下的面积表示为20×30-(30x+20x-x2)米2,则根据题意得:20×30-(30x+20x-x2)=551.
分析 要求修建的路宽,就要设修建的路宽应为x米,根据题意可知:矩形地面-所修路面积=耕地面积,依此列出等量关系解方程即可.
解答 解:设修建的路宽为x米.余下的面积表示为:20×30-(30x+20x-x2)米2,
则列方程为:20×30-(30x+20x-x2)=551,
故答案为:x,20×30-(30x+20x-x2),20×30-(30x+20x-x2)=551.
点评 此题主要考查了有实际问题抽象出一元二次方程,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.注意:矩形面积在减路的面积时,20x+30x中有一个小正方形的面积是重复计算的,所以要再减去x×x面积.

练习册系列答案
相关题目
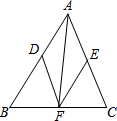 △ABC中,DF∥AC,EF∥AB,AF平分∠BAC.
△ABC中,DF∥AC,EF∥AB,AF平分∠BAC.
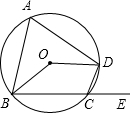 如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于69°.
如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于69°. 如图,△ABC与△A′B′C′关于点O成中心对称,∠ABC=45°,∠B′C′A′=80°,∠BAC=55°.
如图,△ABC与△A′B′C′关于点O成中心对称,∠ABC=45°,∠B′C′A′=80°,∠BAC=55°.