题目内容
7．在△ABC中，已知∠A≤∠B≤∠C，2∠B=5∠A，求∠B的取值范围．分析 由2∠B=5∠A，得到∠A=$\frac{2}{5}$∠B，再根据三角形的内角和定理得∠C=180°-∠A-∠B=180°-$\frac{7}{5}$∠B，而∠A≤∠B≤∠C，则∠B≤180°-$\frac{7}{5}$∠B，即可得到∠B的取值范围．
解答 解：∵2∠B=5∠A，
∴∠A=$\frac{2}{5}$∠B，
∵∠A+∠B+∠C=180°，
∴∠C=180°-∠A-∠B=180°-$\frac{7}{5}$∠B，
又∵∠A≤∠B≤∠C，
∴∠B≤180°-$\frac{7}{5}$∠B，
解得∠B≤75°．
故∠B的取值范围是0°＜∠B≤75°．
点评 本题考查了三角形的内角和定理：三角形的三个内角的和为180°．也考查了不等式的解法．
练习册系列答案
相关题目
17．
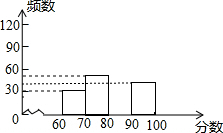某中学组织全校1500名学生参加安全知识测试，为了解本次测试成绩的分别情况，从中随机抽取了部分学生的成绩，绘制出如图不完整的统计图表：
请根据以上图表提供的信息，解答下列问题：
（1）表中m的值为200，n的值为0.25；
（2）补全频数分布直方图；
（3）测试成绩的中位数落在哪个分数段？
（4）规定测试成绩80分以上（含80分）为合格，请估计全校学生中合格人数约有多少人？
某中学组织全校1500名学生参加安全知识测试，为了解本次测试成绩的分别情况，从中随机抽取了部分学生的成绩，绘制出如图不完整的统计图表：| 分数段 | 频数 | 频率 |
| 60≤x＜70 | 30 | 0.15 |
| 70≤x＜80 | 50 | n |
| 80≤x＜90 | 80 | 0.4 |
| 90≤x＜100 | 40 | 0.2 |
| 合计 | m | 1 |
（1）表中m的值为200，n的值为0.25；
（2）补全频数分布直方图；
（3）测试成绩的中位数落在哪个分数段？
（4）规定测试成绩80分以上（含80分）为合格，请估计全校学生中合格人数约有多少人？
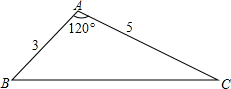已知：如图所示，求BC、tanB．
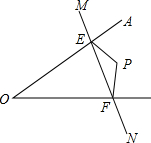如图，点P在∠AOB内部，点M，N分别是点P关于直线AO、BO的对称点，若△PEF的周长为15，求MN的长．