题目内容
 如图,已知:过△ABC的底边BC的中点D任作一条直线交AC于点Q,交AB的延长线于点P,作AE∥BC交DQ的延长线于点E.求证:PD•QE=DQ•PE.
如图,已知:过△ABC的底边BC的中点D任作一条直线交AC于点Q,交AB的延长线于点P,作AE∥BC交DQ的延长线于点E.求证:PD•QE=DQ•PE.考点:平行线分线段成比例
专题:证明题
分析:首先由AE∥BC,得出△PBD∽△PAE,△DCQ∽△EAQ,得出PD:PE=BD:AE,DQ:EQ=CD:AE,进一步由D为BC的中点得出BD=CD,等量代换得出PD:PE=DQ:EQ,整理得出答案即可.
解答:证明:∵AE∥BC,
∴△PBD∽△PAE,△DCQ∽△EAQ,
∴PD:PE=BD:AE,DQ:EQ=CD:AE,
∵D为BC的中点,
∴BD=CD,
∴PD:PE=DQ:EQ,
∴PD•QE=DQ•PE.
∴△PBD∽△PAE,△DCQ∽△EAQ,
∴PD:PE=BD:AE,DQ:EQ=CD:AE,
∵D为BC的中点,
∴BD=CD,
∴PD:PE=DQ:EQ,
∴PD•QE=DQ•PE.
点评:此题考查三角形相似的判定与性质,由平行得出相似是基本的判定方法,进一步利用性质得出结论解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕A点按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角最小等于
如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕A点按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角最小等于 如图所示,A、B、C、D是⊙O上顺次四点,若∠AOC=160°,则∠D=
如图所示,A、B、C、D是⊙O上顺次四点,若∠AOC=160°,则∠D=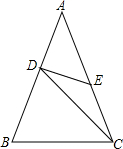 如图,在△ABC中,AB=AC,AD=ED=EC,CD=BC,求△ABC各角的度数.(提示:设∠DCE=x)
如图,在△ABC中,AB=AC,AD=ED=EC,CD=BC,求△ABC各角的度数.(提示:设∠DCE=x)