题目内容
观察下列运算并填空:
32-12=8×1
52-32=8×2;
72-52=8×3;
…
根据以上等式发现规律,用代数式表示这个规律为 .
32-12=8×1
52-32=8×2;
72-52=8×3;
…
根据以上等式发现规律,用代数式表示这个规律为
考点:规律型:数字的变化类
专题:
分析:等式的左边是两个连续奇数的平方差,右边是这两个连续奇数的和除以4的商的8倍.
解答:解:∵32-12═8×1=8×
,
52-32=8×2=8×
,
72-52=8×3=8×
,
…
∴设n(n≥1)表示自然数,用关于n的等式表示这个规律为:(2n+1)2-(2n-1)2=8×
=8n,
即(2n+1)2-(2n-1)2=8n.
故答案为:(2n+1)2-(2n-1)2=8n.
| 3+1 |
| 4 |
52-32=8×2=8×
| 5+3 |
| 4 |
72-52=8×3=8×
| 7+5 |
| 4 |
…
∴设n(n≥1)表示自然数,用关于n的等式表示这个规律为:(2n+1)2-(2n-1)2=8×
| 2n+1+2n-1 |
| 4 |
即(2n+1)2-(2n-1)2=8n.
故答案为:(2n+1)2-(2n-1)2=8n.
点评:本题考查了规律型:数字的变化类,观察等式的规律时,既要分别观察等式的左边和右边,还要注意两边之间的联系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
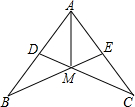 如图,AB=AC,AD=AE,∠BAC=60°,∠C=25°,则∠BMD的度数为( )
如图,AB=AC,AD=AE,∠BAC=60°,∠C=25°,则∠BMD的度数为( )| A、50° | B、65° |
| C、70° | D、85° |
如图是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,…,按此规律,则第10个图形中基础图形的个数是( )


| A、27 | B、30 | C、31 | D、60 |
两条直线被第三条直线所截,若有一对内错角相等,则这对内错角的角平分线( )
| A、互相垂直 |
| B、相交但不垂直 |
| C、互相平行 |
| D、位置关系无法确定 |
 如图,已知正方形ABCD中,E是BC的中点,F是CD上一点,且FD=3CF,试判断△AEF的形状,并说明理由.
如图,已知正方形ABCD中,E是BC的中点,F是CD上一点,且FD=3CF,试判断△AEF的形状,并说明理由. 如图,△ABT是等腰直角三角形,AB是⊙O的直径,且AB=4,则图中阴影部分的面积是
如图,△ABT是等腰直角三角形,AB是⊙O的直径,且AB=4,则图中阴影部分的面积是 如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个n边形(n≥4)木架在同一平面内不变形,至少还要再钉上几根木条?
如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个n边形(n≥4)木架在同一平面内不变形,至少还要再钉上几根木条?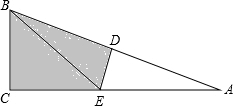 如图,在Rt△ABC中,∠C=90°,△ABC沿DE折叠,使得点A落在点B处,已知AC=6,BC=2,则四边形BCED的面积为
如图,在Rt△ABC中,∠C=90°,△ABC沿DE折叠,使得点A落在点B处,已知AC=6,BC=2,则四边形BCED的面积为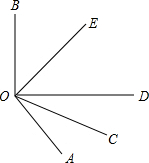 如图,OC是∠AOD的平分线,OE是∠BOD的平分线,∠AOB=130°.
如图,OC是∠AOD的平分线,OE是∠BOD的平分线,∠AOB=130°.