题目内容
20.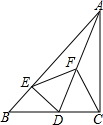 如图,在Rt△ABC中,∠ACB=90°,D是边BC上一动点(不与B,C重合),DE⊥AB于点E,点F是线段AD的中点,连接EF,CF.
如图,在Rt△ABC中,∠ACB=90°,D是边BC上一动点(不与B,C重合),DE⊥AB于点E,点F是线段AD的中点,连接EF,CF.(1)试猜想线段EF与CF的大小关系,并加以证明.
(2)若∠BAC=30°,连接CE,在D点运动过程中,探求CE与AD的数量关系.
分析 (1)EF和CF分别是直角△AED和直角△ACD斜边上的中线,依据直角三角形斜边上的中线等于斜边的一半即可证得;
(2)证明△EFC是等边三角形,然后根据等边三角形的定义以及直角三角形的性质求解.
解答  解:(1)EF=CF,
解:(1)EF=CF,
在Rt△AED和Rt△ACD中,
∵点F是线段AD的中点,
∴EF=$\frac{1}{2}$ AD,CF=$\frac{1}{2}$AD,
∴EF=CF.
(2)由(1)可知EF=AF=CF,
∴∠AEF=∠EAF,∠ACF=∠CAF,
∴∠EFD=2∠EAF,∠CFD=2∠CAF,
∴∠EFC=2∠BAC=60°,
又EF=CF,
∴△EFC为等边三角形,
∴CE=EF=$\frac{1}{2}$ AD.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半以及等边三角形的判定与性质,证得△EFC是等边三角形是关键.

练习册系列答案
相关题目
9.一辆汽车在公路上行驶,其所走的路程和所用的时间可用下表表示:
(1)在这个变化过程中,自变量、因变量各是什么?
(2)当汽车行驶路程s为20km时,所花的时间t是多少分钟?
(3)从表中说出随着t逐渐变大,s的变化趋势是什么?
(4)如果汽车行驶的时间为t(min),行驶的路程为s(km),那么路程s与时间t之间的关系式为s=2t.
(5)按照这一行驶规律,当所花的时间t是300min时,汽车行驶的路程s是多少千米?
| 时间/t(min) | 1 | 2.5 | 5 | 10 | 20 | 50 | … |
| 路程/s(km) | 2 | 5 | 10 | 20 | 40 | 100 | … |
(2)当汽车行驶路程s为20km时,所花的时间t是多少分钟?
(3)从表中说出随着t逐渐变大,s的变化趋势是什么?
(4)如果汽车行驶的时间为t(min),行驶的路程为s(km),那么路程s与时间t之间的关系式为s=2t.
(5)按照这一行驶规律,当所花的时间t是300min时,汽车行驶的路程s是多少千米?
7.已知$\sqrt{a+2}$+|b-1|=0,那么(a+b)2017的值为( )
| A. | -1 | B. | 1 | C. | 32017 | D. | -32017 |
 B.
B.  C.
C.  D.
D. 
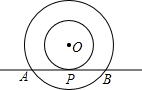 如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点P.
如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点P.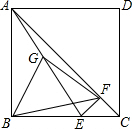 在正方形ABCD中.
在正方形ABCD中.
