题目内容
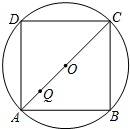 如图,正方形ABCD内接于⊙O,Q是直径AC上的一个动点,连接DQ并延长交⊙O于P.若QP=QO,则
如图,正方形ABCD内接于⊙O,Q是直径AC上的一个动点,连接DQ并延长交⊙O于P.若QP=QO,则| QA |
| QC |
考点:正多边形和圆
专题:
分析:分两种情况①设⊙O的半径为r,QO=m,则QP=m,QC=r+m,QA=r-m.②设⊙O的半径为r,QO=m,则QP=m,
QC=m,QA=r+m,分别利用相交弦定理,求出m与r的关系,即用r表示出m,即可表示出所求比值.
QC=m,QA=r+m,分别利用相交弦定理,求出m与r的关系,即用r表示出m,即可表示出所求比值.
解答:解:①如图1,设⊙O的半径为r,QO=m,则QP=m,QC=r+m,QA=r-m.
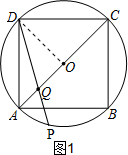
在⊙O中,根据相交弦定理,得QA•QC=QP•QD.
即(r-m)(r+m)=m•QD,所以QD=
.
连接DO,由勾股定理,得QD2=DO2+QO2,
即(
)2=r2+m2,
解得m=
r.
所以
=
=
=2-
.
②如图2,设⊙O的半径为r,QO=m,则QP=m,QC=m,QA=r+m.
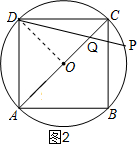
在⊙O中,根据相交弦定理,得QA•QC=QP•QD.
即(r+m)(r-m)=m•QD,所以QD=
.
连接DO,由勾股定理,得QD2=DO2+QO2,
即(
)2=r2+m2,
解得m=
r.
所以
=
=
=2+
.
故答案为:2-
,或2-
.

在⊙O中,根据相交弦定理,得QA•QC=QP•QD.
即(r-m)(r+m)=m•QD,所以QD=
| r2-m2 |
| m |
连接DO,由勾股定理,得QD2=DO2+QO2,
即(
| r2-m2 |
| m |
解得m=
| ||
| 3 |
所以
| QA |
| QC |
| r-m |
| r+m |
| ||
|
| 3 |
②如图2,设⊙O的半径为r,QO=m,则QP=m,QC=m,QA=r+m.

在⊙O中,根据相交弦定理,得QA•QC=QP•QD.
即(r+m)(r-m)=m•QD,所以QD=
| r2-m2 |
| m |
连接DO,由勾股定理,得QD2=DO2+QO2,
即(
| r2-m2 |
| m |
解得m=
| ||
| 3 |
所以
| QA |
| QC |
| r+m |
| r-m |
| ||
|
| ||
|
| 3 |
故答案为:2-
| 3 |
| 3 |
点评:本题考查了相交弦定理,即“圆内两弦相交于圆内一点,各弦被这点所分得的两线段的长的乘积相等”.熟记并灵活应用定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 细心观察图形,认真分析各式,然后解答问题.
细心观察图形,认真分析各式,然后解答问题. 画图:牧童在A处放牛,其家在B处,若牧童从A处将牛牵到河边C处饮水后再回家,试问C在何处,所走路程最短?(保留作图痕迹)
画图:牧童在A处放牛,其家在B处,若牧童从A处将牛牵到河边C处饮水后再回家,试问C在何处,所走路程最短?(保留作图痕迹)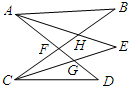 如图,AD、BC相交于点F,AE、CE分别平分∠BAD、∠DCB,若∠B=25°,∠D=35°,则∠E的度数为
如图,AD、BC相交于点F,AE、CE分别平分∠BAD、∠DCB,若∠B=25°,∠D=35°,则∠E的度数为 如图,△ABC中.AB=AC=10,BC=16,⊙A的半径为6,判断⊙A与BC的位置关系,并证明你的结论.
如图,△ABC中.AB=AC=10,BC=16,⊙A的半径为6,判断⊙A与BC的位置关系,并证明你的结论.