题目内容
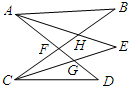 如图,AD、BC相交于点F,AE、CE分别平分∠BAD、∠DCB,若∠B=25°,∠D=35°,则∠E的度数为
如图,AD、BC相交于点F,AE、CE分别平分∠BAD、∠DCB,若∠B=25°,∠D=35°,则∠E的度数为考点:三角形内角和定理,三角形的外角性质
专题:
分析:先根据∠AFC是△ABF与△CDF的外角得出,∠B+∠BAD=∠D+∠DCB,再根据AE、CE分别平分∠BAD、∠DCB得出∠BAE=∠EAD=
∠BAD,∠DCE=∠BCE=
∠BCD,根据三角形外角的性质即可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵∠AFC是△ABF与△CDF的外角,
∴∠B+∠BAD=∠D+∠DCB.
∵AE、CE分别平分∠BAD、∠DCB,
∴∠BAE=∠EAD=
∠BAD,∠DCE=∠BCE=
∠BCD.
∵∠AHC是△ABH与△CEH的外角,
∴∠E+
∠DAB=∠D+
∠DCB①,
同理可得,∠E+
∠DCB=∠B+
∠BAD②,
①+②得,2∠E=∠B+∠D,
∵∠B=25°,∠D=35°,
∴∠E=
(25°+35°)=30°.
故答案为:30°.
∴∠B+∠BAD=∠D+∠DCB.
∵AE、CE分别平分∠BAD、∠DCB,
∴∠BAE=∠EAD=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AHC是△ABH与△CEH的外角,
∴∠E+
| 1 |
| 2 |
| 1 |
| 2 |
同理可得,∠E+
| 1 |
| 2 |
| 1 |
| 2 |
①+②得,2∠E=∠B+∠D,
∵∠B=25°,∠D=35°,
∴∠E=
| 1 |
| 2 |
故答案为:30°.
点评:本题考查的是三角形外角的性质,熟知三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 将1,2,3,4,…,16这16个自然数分别放在正方形的四条边上,每条边上四个数的和相等,依次填数是多少?
将1,2,3,4,…,16这16个自然数分别放在正方形的四条边上,每条边上四个数的和相等,依次填数是多少?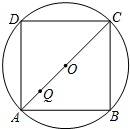 如图,正方形ABCD内接于⊙O,Q是直径AC上的一个动点,连接DQ并延长交⊙O于P.若QP=QO,则
如图,正方形ABCD内接于⊙O,Q是直径AC上的一个动点,连接DQ并延长交⊙O于P.若QP=QO,则 如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为a个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按
如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为a个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按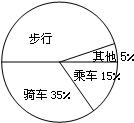 某校对全校2560名学生的上学方式进行了一次抽样调查,右图是根据此次调查结果所绘制的一个未完成的扇形统计图,被调查的学生中骑车的有21人,则下列四种说法:
某校对全校2560名学生的上学方式进行了一次抽样调查,右图是根据此次调查结果所绘制的一个未完成的扇形统计图,被调查的学生中骑车的有21人,则下列四种说法: