题目内容
 细心观察图形,认真分析各式,然后解答问题.
细心观察图形,认真分析各式,然后解答问题.OA22=(
| 1 |
| ||
| 2 |
OA32=12+(
| 2 |
| ||
| 2 |
OA42=12+(
| 3 |
| ||
| 2 |
(1)推算出OA10的长.
(2)求出S12+S22+S23+…+S210的值.
考点:算术平方根,勾股定理
专题:规律型
分析:(1)根据规律写出OA102,再根据算术平方根的定义解答;
(2)根据分析写出算式,然后利用求和公式列式计算即可得解.
(2)根据分析写出算式,然后利用求和公式列式计算即可得解.
解答:解:(1)∵OA22=(
)2+1=2,
OA32=12+(
)2=3,
OA42=12+(
)2=4,
…,
∴OA102=10,
∴OA10=
;
(2)S12+S22+S23+…+S210
=
+
+
+…+
=
×(1+2+3+…+10)
=
×
=
.
| 1 |
OA32=12+(
| 2 |
OA42=12+(
| 3 |
…,
∴OA102=10,
∴OA10=
| 10 |
(2)S12+S22+S23+…+S210
=
| 1 |
| 4 |
| 2 |
| 4 |
| 3 |
| 4 |
| 10 |
| 4 |
=
| 1 |
| 4 |
=
| 1 |
| 4 |
| 10×(10+1) |
| 2 |
=
| 55 |
| 4 |
点评:本题考查了算术平方根,勾股定理,根据数字的变化规律,观察出被开方数的变化规律是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
若α,β是一元二次方程x2-3x+1=0的两根,则α2+β2的值是( )
| A、6 | B、7 | C、8 | D、9 |
 如图,在△ABC和△ABD中,∠ADB=∠ABC=90°,AD=BD,∠BAC=30°,求∠BDC的正切值.
如图,在△ABC和△ABD中,∠ADB=∠ABC=90°,AD=BD,∠BAC=30°,求∠BDC的正切值. 如图,在△ABC中,点D是∠ABC的平分线与∠ACB的外角平分线的交点,DE∥BC,交AB于E,交AC于F.
如图,在△ABC中,点D是∠ABC的平分线与∠ACB的外角平分线的交点,DE∥BC,交AB于E,交AC于F.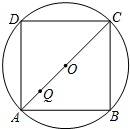 如图,正方形ABCD内接于⊙O,Q是直径AC上的一个动点,连接DQ并延长交⊙O于P.若QP=QO,则
如图,正方形ABCD内接于⊙O,Q是直径AC上的一个动点,连接DQ并延长交⊙O于P.若QP=QO,则