题目内容
 如图,△ABC中.AB=AC=10,BC=16,⊙A的半径为6,判断⊙A与BC的位置关系,并证明你的结论.
如图,△ABC中.AB=AC=10,BC=16,⊙A的半径为6,判断⊙A与BC的位置关系,并证明你的结论.考点:切线的判定
专题:
分析:过A作AD⊥BC,垂足为点D,利用勾股定理求得线段AD的长与⊙O的半径比较后即可确定直线与圆的位置关系.
解答: 解:⊙A与直线BC相交.
解:⊙A与直线BC相交.
过A作AD⊥BC,垂足为点D.
∵AB=AC,BC=16,
∴BD=
BC=
×16=8,
在Rt△ABC中,AB=10,BD=8,
∴AD=
=
=6,
∵⊙O的半径为6,
∴AD=r,
⊙A与直线BC相切.
 解:⊙A与直线BC相交.
解:⊙A与直线BC相交. 过A作AD⊥BC,垂足为点D.
∵AB=AC,BC=16,
∴BD=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ABC中,AB=10,BD=8,
∴AD=
| AB2-BD2 |
| 102-82 |
∵⊙O的半径为6,
∴AD=r,
⊙A与直线BC相切.
点评:本题考查了直线与圆的位置关系,解题的关键是求得圆心到直线的距离.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
若α,β是一元二次方程x2-3x+1=0的两根,则α2+β2的值是( )
| A、6 | B、7 | C、8 | D、9 |
 如图,在△ABC和△ABD中,∠ADB=∠ABC=90°,AD=BD,∠BAC=30°,求∠BDC的正切值.
如图,在△ABC和△ABD中,∠ADB=∠ABC=90°,AD=BD,∠BAC=30°,求∠BDC的正切值.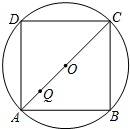 如图,正方形ABCD内接于⊙O,Q是直径AC上的一个动点,连接DQ并延长交⊙O于P.若QP=QO,则
如图,正方形ABCD内接于⊙O,Q是直径AC上的一个动点,连接DQ并延长交⊙O于P.若QP=QO,则 如图,AC是⊙O的弦,以OA为直径的圆交AC于点E.
如图,AC是⊙O的弦,以OA为直径的圆交AC于点E.
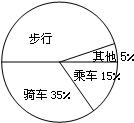 某校对全校2560名学生的上学方式进行了一次抽样调查,右图是根据此次调查结果所绘制的一个未完成的扇形统计图,被调查的学生中骑车的有21人,则下列四种说法:
某校对全校2560名学生的上学方式进行了一次抽样调查,右图是根据此次调查结果所绘制的一个未完成的扇形统计图,被调查的学生中骑车的有21人,则下列四种说法: 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数是
如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数是