题目内容
9.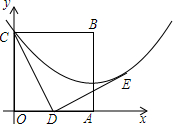 边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点 E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.
边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点 E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.(1)求E点坐标;
(2)设抛物线的解析式为y=a(x-h)2+k,求a,h,k;
(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点M,N的坐标;若不存在,请说明理由.
分析 (1)过点E作EF⊥x轴于点F,证△COD≌△DFE即可;
(2)直线AB就是对称轴,确定了h,算出C、E两点坐标,代入抛物线解析式,确定a、k;
(3)分三种情况讨论:N在抛物线顶点处;N在抛物线对称轴左侧;N在抛物线对称轴右侧.
解答 解:(1)过点E作EF⊥x轴于点F,如图1,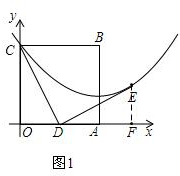
∵DE⊥DC,
∴∠CDO+∠EDF=90°,
∵∠CDO+∠OCD=90°,
∴∠OCD=∠EDF,
在△COD和△DFE中
$\left\{\begin{array}{l}{∠OCD=∠FDE}\\{∠COD=∠DFE}\\{CD=DE}\end{array}\right.$
∴△COD≌△DFE(AAS),
∴OD=EF,DF=CO,
∵CO=OA=2,D为OA中点,
∴EF=OD=DA=1,DF=OC=2,
∴E(3,1);
(2)∵抛物线y=a(x-h)2+k以AB为对称轴,
∴h=2,
∵y=a(x-h)2+k经过C(0,2)和E(3,1)两点,
∴$\left\{\begin{array}{l}{4a+k=2}\\{a+k=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{k=\frac{2}{3}}\end{array}\right.$;
(3)①若以DE为平行四边形的对角线,如图2,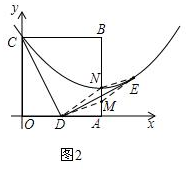
此时,N点就是抛物线的顶点(2,$\frac{2}{3}$),
由N、E两点坐标可求得直线NE的解析式为:y=$\frac{1}{3}$x;
∵DM∥EN,
∴设DM的解析式为:y=$\frac{1}{3}x+b$,
将D(1,0)代入可求得b=-$\frac{1}{3}$,
∴DM的解析式为:y=$\frac{1}{3}x-\frac{1}{3}$,
令x=2,则y=$\frac{1}{3}$,
∴M(2,$\frac{1}{3}$);
②过点C作CM∥DE交抛物线对称轴于点M,连接ME,如图3,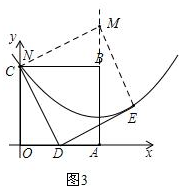
∵CM∥DE,DE⊥CD,
∴CM⊥CD,
∵OC⊥CB,
∴∠OCD=∠BCM,
在△OCD和△BCM中
$\left\{\begin{array}{l}{∠BCM=∠OCD}\\{∠CBM=∠COD}\\{CO=CB}\end{array}\right.$,
∴△OCD≌△BCM(ASA),
∴CM=CD=DE,BM=OD=1,
∴CDEM是平行四边形,
即N点与C占重合,
∴N(0,2),M(2,3);
③N点在抛物线对称轴右侧,MN∥DE,如图4,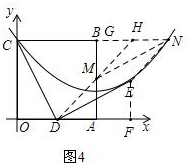
作NG⊥BA于点G,延长DM交BN于点H,
∵MNED是平行四边形,
∴∠MDE=MNE,∠ENH=∠DHB,
∵BN∥DF,
∴∠ADH=∠DHB=∠ENH,
∴∠MNB=∠EDF,
在△BMN和△FED中
$\left\{\begin{array}{l}{∠MBN=∠EFD}\\{∠BNM=∠FDE}\\{MN=DE}\end{array}\right.$
∴△BMN≌△FED(AAS),
∴BM=EF=1,
BN=DF=2,
∴M(2,1),N(4,2);
综上所述,N、M分别以下组合时,以点M,N,D,E为顶点的四边形是平行四边形
N(2,$\frac{2}{3}$),M(2,$\frac{1}{3}$);
N(0,2),M(2,3);
M(2,1),N(4,2).
点评 本题考查了全等三角形的判定与性质、待定系数法求二次函数解析式、待定系数法求一次函数解析式、平行四边形的判定与性质等知识点,综合性较强,有一定难度.第(3)问体现分类讨论的数学思想,注意不要漏解.

 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案| A. | b3•b3=2b3 | B. | (2x5)2=2x10 | C. | (-xy6)2=x2y12 | D. | x5•x2=x10 |
(1)x+1;(2)$\frac{1}{x}$;(3)πr2;(4)-$\frac{3}{2}$a2b;(5)-32x2y3.
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
| A. | -3ab2c3与0.6c3b2a | B. | 1与$\frac{1}{8}$ | ||
| C. | 2x2y与-2x2y | D. | x3与3x |
 在Rt△ABC中,∠ABC=90°,AC=6,P、Q分别为AC、BC的中点,AQ、BP相交于点O,则OP=1.
在Rt△ABC中,∠ABC=90°,AC=6,P、Q分别为AC、BC的中点,AQ、BP相交于点O,则OP=1.