题目内容
16.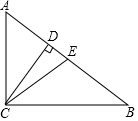 如图,在Rt△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,若AC=CE=6,则CD的长为( )
如图,在Rt△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,若AC=CE=6,则CD的长为( )| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 6 | D. | 6$\sqrt{3}$ |
分析 根据条件可求得AC=AE=CE=BE,可证得△ACE为等边三角形,可求得DE=$\frac{1}{2}$AE,可求得DE,则可求得CD.
解答 解:∵∠ACB=90°,CE为斜边上的中线,
∴AE=BE=CE=AC=6
∴△ACE为等边三角形,
∴∠AEC=60°,
∴∠DCE=30°,
∵CD⊥AE,
∴DE=$\frac{1}{2}$AE=3,
∴CD=$\sqrt{3}$DE=3$\sqrt{3}$,
故选B.
点评 本题主要考查直角三角形的性质及等边三角形的性质,根据直角三角形的性质求得BE、根据等边三角形的性质求得DE是解题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
6.下面各数中,比-1大的数是( )
| A. | -5 | B. | -$\frac{3}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
11.下列等式一定成立的是( )
| A. | a2+a2=a5 | B. | (a-1)2=a2-1 | C. | (-a)9÷(-a)3=a6 | D. | (-2a2)3=8a6 |
1.将直线y=$\frac{1}{2}$x+1向右平移4个单位后得到直线y=kx+b,则k+b的值为( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
8.下列图形中,不是中心对称图形的是( )
| A. | 平行四边形 | B. | 圆 | C. | 等边三角形 | D. | 正六边形 |
6.有大小两种货车,2辆大货车与3辆小货车一次可以运货16吨,6辆小货车比2辆大货车一次可以多运2吨.设一辆大货车一次可以运货x吨,一辆小货车一次可以运货y吨,根据题意所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{2x+3y=16}\\{6x-2y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+3y=16}\\{6y-2x=2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{3x+2y=16}\\{6x-2y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+3y=2}\\{6x-2y=16}\end{array}\right.$ |
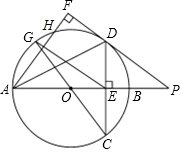 如图,在⊙O中,直径AB垂直弦CD于E,过点D作弦AH的垂线,垂足为F,交AB的延长线于点P.
如图,在⊙O中,直径AB垂直弦CD于E,过点D作弦AH的垂线,垂足为F,交AB的延长线于点P.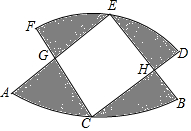 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是$\widehat{AB}$的中点,若扇形的半径为3,则图中阴影部分的面积等于$\frac{9π}{2}$-9.
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是$\widehat{AB}$的中点,若扇形的半径为3,则图中阴影部分的面积等于$\frac{9π}{2}$-9.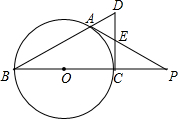 如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD得中点E,AE的延长线与BC的延长线交于点P.
如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD得中点E,AE的延长线与BC的延长线交于点P.