题目内容
6.有大小两种货车,2辆大货车与3辆小货车一次可以运货16吨,6辆小货车比2辆大货车一次可以多运2吨.设一辆大货车一次可以运货x吨,一辆小货车一次可以运货y吨,根据题意所列方程组正确的是( )| A. | $\left\{\begin{array}{l}{2x+3y=16}\\{6x-2y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+3y=16}\\{6y-2x=2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{3x+2y=16}\\{6x-2y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+3y=2}\\{6x-2y=16}\end{array}\right.$ |
分析 根据题意可得等量关系:2辆大货车运的吨数+3辆小货车运的吨数=16吨;6辆小货车运的吨数-2辆大货车运的吨数=2吨,根据等量关系列出方程组即可.
解答 解:设一辆大货车一次可以运货x吨,一辆小货车一次可以运货y吨,根据题意得:
$\left\{\begin{array}{l}{2x+3y=16}\\{6y-2x=2}\end{array}\right.$,
故选:B.
点评 此题主要考查了由实际问题抽象出二元一次方程,关键是正确理解题意,找出题目中的等量关系,列出方程组.

练习册系列答案
相关题目
16.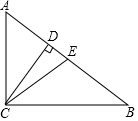 如图,在Rt△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,若AC=CE=6,则CD的长为( )
如图,在Rt△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,若AC=CE=6,则CD的长为( )
 如图,在Rt△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,若AC=CE=6,则CD的长为( )
如图,在Rt△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,若AC=CE=6,则CD的长为( )| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 6 | D. | 6$\sqrt{3}$ |
17. 已知一次函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b>1的解集为( )
已知一次函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b>1的解集为( )
 已知一次函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b>1的解集为( )
已知一次函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b>1的解集为( )| A. | x<0 | B. | x>0 | C. | x<2 | D. | x>2 |
14.正多边形的中心角是30°,那么这个正多边形的边数是( )
| A. | 12 | B. | 10 | C. | 8 | D. | 6 |
1.计算正确的是( )
| A. | x2+x2=x4 | B. | x2+y2=x2y2 | C. | x2•x2=2x4 | D. | (xy2)2=x2y4 |
11. 实数a,b,c在数轴上对应点的位置大致如图所示,则下列式子成立的是( )
实数a,b,c在数轴上对应点的位置大致如图所示,则下列式子成立的是( )
 实数a,b,c在数轴上对应点的位置大致如图所示,则下列式子成立的是( )
实数a,b,c在数轴上对应点的位置大致如图所示,则下列式子成立的是( )| A. | ac>bc | B. | |a-b|=a-b | C. | -a<-b | D. | a-c<b-c |
15.一元二次方程x2-2x=0根的判别式的值为( )
| A. | 4 | B. | 2 | C. | 0 | D. | -4 |
16.在下列的计算中,正确的是( )
| A. | m3+m2=m5 | B. | m5÷m2=m3 | C. | (2m)3=6m3 | D. | (m+1)2=m2+1 |



