题目内容
若
+
+
=1,求abc的值.
| a |
| ab+a+1 |
| b |
| bc+b+1 |
| c |
| ac+c+1 |
考点:对称式和轮换对称式,完全平方式,整式的混合运算,分式的加减法
专题:
分析:将方程进行变形、简化、去分母、整理后,就可求出abc的值.
解答:解:∵
+
+
=1,
∴
+
=1-
=
,
∴
=
-
=
=
=
,
∴a(ac+c+1)(bc+b+1)=(ab+a+1)(abc2+ac+1),
∴(a2c+ac+a)(bc+b+1)=(ab+a+1)(abc2+ac+1),
∴a2bc2+a2bc+a2c+abc2+abc+ac+abc+ab+a=a2b2c2+a2bc+ab+a2bc2+a2c+a+abc2+ac+1,
整理得:a2b2c2-2abc+1=0,
∴(abc-1)2=0,
解得:abc=1.
∴abc的值为1.
| a |
| ab+a+1 |
| b |
| bc+b+1 |
| c |
| ac+c+1 |
∴
| a |
| ab+a+1 |
| b |
| bc+b+1 |
| c |
| ac+c+1 |
| ac+1 |
| ac+c+1 |
∴
| a |
| ab+a+1 |
| ac+1 |
| ac+c+1 |
| b |
| bc+b+1 |
=
| (ac+1)(bc+b+1)-b(ac+c+1) |
| (ac+c+1)(bc+b+1) |
=
| abc2+abc+ac+bc+b+1-abc-bc-b |
| (ac+c+1)(bc+b+1) |
=
| abc2+ac+1 |
| (ac+c+1)(bc+b+1) |
∴a(ac+c+1)(bc+b+1)=(ab+a+1)(abc2+ac+1),
∴(a2c+ac+a)(bc+b+1)=(ab+a+1)(abc2+ac+1),
∴a2bc2+a2bc+a2c+abc2+abc+ac+abc+ab+a=a2b2c2+a2bc+ab+a2bc2+a2c+a+abc2+ac+1,
整理得:a2b2c2-2abc+1=0,
∴(abc-1)2=0,
解得:abc=1.
∴abc的值为1.
点评:本题考查了分式的加减运算、整式的混合运用、完全平方公式等知识,对运算能力的要求比较高.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设x=
,y=(-
)2,那么2x+y等于( )
| (-5)2 |
| 5 |
| A、5 | B、-5 | C、15 | D、-15 |
当x=2时,ax+3的值是5,当x=-2时,代数式ax+3的值是( )
| A、-5 | B、1 | C、-1 | D、2 |
在一次全国足球甲A比赛中,大连万达队保持前11轮(场)连续不败的记录,共积分23分,按比赛规则,胜1场得3分,平一场得1分,求万达队共胜了多少场?若设万达队共胜了x场,平了y场,则列出的方程组是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
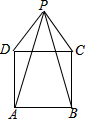 如图,P为正方形ABCD外一点,且∠PAD=∠PBC=15°,求证:△PDC为等边三角形.
如图,P为正方形ABCD外一点,且∠PAD=∠PBC=15°,求证:△PDC为等边三角形. 如图,在△ABC中,AB=2014,AC=2012,AD为中线,则△ABD与△ACD的周长之差为
如图,在△ABC中,AB=2014,AC=2012,AD为中线,则△ABD与△ACD的周长之差为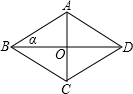 如图,菱形ABCD中对角线AC=16,BD=30,求:
如图,菱形ABCD中对角线AC=16,BD=30,求: