题目内容
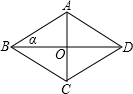 如图,菱形ABCD中对角线AC=16,BD=30,求:
如图,菱形ABCD中对角线AC=16,BD=30,求:(1)∠ABD的四个三角函数;
(2)求sin∠ABC.
考点:菱形的性质,解直角三角形
专题:
分析:(1)由菱形ABCD中对角线AC=16,BD=30,可求得OA,OB,继而由勾股定理,可求得AB的长,继而求得∠ABD的四个三角函数;
(2)首先过点A作AE⊥BC于点E,利用菱形的面积,即可求得AE的长,继而求得答案.
(2)首先过点A作AE⊥BC于点E,利用菱形的面积,即可求得AE的长,继而求得答案.
解答: 解:(1)∵菱形ABCD中对角线AC=16,BD=30,
解:(1)∵菱形ABCD中对角线AC=16,BD=30,
∴OA=
AC=8,OB=
BD=15,AC⊥BD,
∴AB=
=17,
∴sin∠ABD=
=
,cos∠ABD=
=
,tan∠ABD=
=
,cot∠ABD=
=
;
(2)过点A作AE⊥BC于点E,
∵S菱形ABCD=
AC•BD=
×16×30=240,
∴AE=
=
,
∴sin∠ABC=
=
.
 解:(1)∵菱形ABCD中对角线AC=16,BD=30,
解:(1)∵菱形ABCD中对角线AC=16,BD=30,∴OA=
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=
| OA2+OB2 |
∴sin∠ABD=
| OA |
| AB |
| 8 |
| 17 |
| OB |
| AB |
| 15 |
| 17 |
| OA |
| OB |
| 8 |
| 15 |
| OB |
| OA |
| 15 |
| 8 |
(2)过点A作AE⊥BC于点E,
∵S菱形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=
| S菱形ABCD |
| BC |
| 240 |
| 17 |
∴sin∠ABC=
| AE |
| AB |
| 240 |
| 289 |
点评:此题考查了菱形的性质、勾股定理以及三角函数的定义.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
下列计算正确的是( )
| A、-32-(-23)=1 | ||||
B、6÷3×
| ||||
C、
| ||||
D、(1
|