题目内容
20.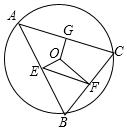 如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O,分别作AB、BC、AC的垂线,垂足分别为E、F、G,连接EF,若OG=3,则EF为4.
如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O,分别作AB、BC、AC的垂线,垂足分别为E、F、G,连接EF,若OG=3,则EF为4.
分析 连接OA,根据勾股定理和垂径定理求出AC,根据三角形中位线定理求出EF.
解答 解: 连接OA,
连接OA,
∵OG⊥AC,
∴∠OGA=90°,AC=2AG,
∴AG=$\sqrt{O{A}^{2}-O{G}^{2}}$=4,
∴AC=2AG=8,
∵OE⊥AB,OF⊥BC,
∴AE=EB,CF=FB,
∴EF=$\frac{1}{2}$AC=4,
故答案为:4.
点评 本题考查的是三角形的外接圆和外心的概念和性质、三角形中位线定理的应用,掌握垂径定理、三角形中位线定理是解题的关键.

练习册系列答案
相关题目
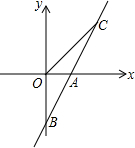 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).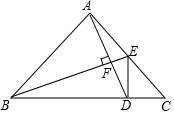 如图,在Rt△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB,D、E分别是BC、AC上的点,若AD⊥BE,∠ADB=∠CDE,CE=2,则S△ADE=$\frac{4}{3}$.
如图,在Rt△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB,D、E分别是BC、AC上的点,若AD⊥BE,∠ADB=∠CDE,CE=2,则S△ADE=$\frac{4}{3}$.