题目内容
4.若二次函数y=ax2+b最大值为4,且该函数的图象经过点A(1,3).(1)a=-1,b=4,顶点D坐标(0,4);
(2)求这个抛物线关于x轴对称后所得的新函数解析式;
(3)是否在抛物线上存在点B,使得S△DOB=2S△AOD?存在的话,请求出B的坐标;不存在的话,请说明理由.
分析 (1)根据待定系数法即可求得a、b,根据顶点式即可得到顶点坐标;
(2)利用原抛物线上的关于x轴对称的点的特点:横坐标相同,纵坐标互为相反数就可以解答.
(3)假设存在并设出其坐标,根据三角形面积相等易得|x|=2,分x的值为2与-2两种情况讨论,进而可得答案.
解答 解:(1)∵二次函数y=ax2+b最大值为4,
∴b=4,
∴y=ax2+4,
∵函数的图象经过点A(1,3),
∴3=a+4,解得a=-1,
∴y=-x2+4,
∴顶点D的坐标为(0,4);
故答案为-1,4,0,4;
(2)∵抛物线y=-x2+4关于x轴对称的抛物线为-y=-x2+4,
∴所求解析式为:y=x2-4.
(3)假设存在点B(x,y),
依题意有$\frac{{S}_{△DOB}}{{S}_{△AOD}}$=$\frac{2}{1}$,
∴$\frac{\frac{1}{2}OD×|x|}{\frac{1}{2}OD×1}$=$\frac{2}{1}$,
∴|x|=2,
∴x=±2,
①当x=2时,则y=-x2+4=0
②当x=-2时,则y=-x2+4=0,
∴存在满足条件的点B,它的坐标为:(2,0)或(-2,0).
点评 本题考查了待定系数法求解析式,二次函数的性质,二次函数图象上点的坐标特征,三角形的面积,二次函数图象与几何变换,求得抛物线的解析式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
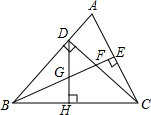 已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,某同学分析图形后得出以下结论:①DH⊥BC;②CE=$\frac{1}{2}BF$;③△AEB≌△CEB;④△BDF≌△CDA.上述结论一定正确的是( )
已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,某同学分析图形后得出以下结论:①DH⊥BC;②CE=$\frac{1}{2}BF$;③△AEB≌△CEB;④△BDF≌△CDA.上述结论一定正确的是( )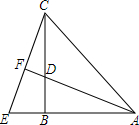 如图,在△ABC中,∠ABC=90°,AB=BC,D是BC上的一点,E是AB延长线上的一点,AD=CE,AD的延长线交CE于点F,则AF与CE垂直吗?为什么?
如图,在△ABC中,∠ABC=90°,AB=BC,D是BC上的一点,E是AB延长线上的一点,AD=CE,AD的延长线交CE于点F,则AF与CE垂直吗?为什么?
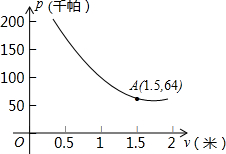 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气体体积V(立方米)的反比例函数,其图象如图所示(千帕是压强单位)
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气体体积V(立方米)的反比例函数,其图象如图所示(千帕是压强单位)