题目内容
14.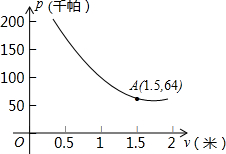 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气体体积V(立方米)的反比例函数,其图象如图所示(千帕是压强单位)
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气体体积V(立方米)的反比例函数,其图象如图所示(千帕是压强单位)(1)写出这个函数的解析式;
(2)当气球的体积是0.8立方米时,气球内的气压是多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米?
分析 (1)设p与V的函数的解析式为p=$\frac{k}{v}$利用待定系数法求函数解析式即可;
(2)把v=0.8代入p=$\frac{96}{v}$可得p=120;
(3)把p=144代入p=$\frac{96}{v}$得,V=$\frac{2}{3}$.所以可知当气球内的气压>144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于$\frac{2}{3}$立方米.
解答 解:(1)设p与V的函数的解析式为p=$\frac{k}{v}$,
把点A(1.5,64)代入,
解得k=96.
∴这个函数的解析式为p=$\frac{96}{v}$;
(2)把v=0.8代入p=$\frac{96}{v}$得:p=120,
当气球的体积为0.8立方米时,气球内的气压是120千帕;
(3)把p=144代入p=$\frac{96}{v}$得,V=$\frac{2}{3}$,
故p≤144时,v≥$\frac{2}{3}$,
答:气球的体积应不小于$\frac{2}{3}$立方米.
点评 此题主要考查了反比例函数的应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式.会用不等式解决实际问题.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
4.下列计算正确的是( )
| A. | (x+y)2=x2+y2 | B. | (x+2y)(x-2y)=x2-2y2 | C. | (x-y)2=x2-2xy-y2 | D. | (-x+y)2=x2-2xy+y2 |