题目内容
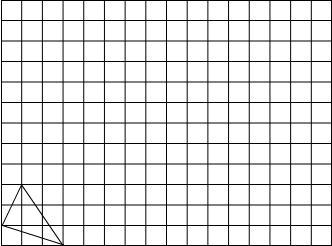
13．用直尺和圆规在如图所示的数轴上作出$\sqrt{13}$的点．
分析 过表示3的点作垂线，再作直角三角形BOC，两直角边长分别为2，3，进而得到斜边长为$\sqrt{13}$，再以O为圆心，OC长为半径画弧与数轴正半轴的交点D即为所求的表示$\sqrt{13}$的位置．
解答 解：$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$，如图所示，
点D即为所求．
点评 此题主要考查勾股定理、实数与数轴、复杂作图中在数轴上表示无理数的作法；熟练掌握勾股定理和基本作图方法是解题关键．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
8．将抛物线y=2（x+1）2-2的图象先向左平移1个单位长度，再向上平移3个单位长度，则顶点坐标为（ ）
| A． | （-2，1） | B． | （2，1） | C． | （0，1） | D． | （-2，-5） |