题目内容
14. 如图,在平面直角坐标系中,A(-8,-1),B(-6,-9),C(-2.-9),D(-4,-1).先将四边形ABCD沿x轴翻折,再向右平移8个单位长度,向下平移1个单位长度后,得到四边形A1B1C1D1,最后将四边形A1B1C1D1,绕着点A1旋转,使旋转后的四边形对角线的交点落在x轴上,则旋转后的四边形对角线的交点坐标为( )
如图,在平面直角坐标系中,A(-8,-1),B(-6,-9),C(-2.-9),D(-4,-1).先将四边形ABCD沿x轴翻折,再向右平移8个单位长度,向下平移1个单位长度后,得到四边形A1B1C1D1,最后将四边形A1B1C1D1,绕着点A1旋转,使旋转后的四边形对角线的交点落在x轴上,则旋转后的四边形对角线的交点坐标为( )| A. | (4,0) | B. | (5,0) | C. | (4,0)或(-4,0) | D. | (5,0)或(-5,0) |
分析 根据题意画出图形,发现有两种情况:①对角线交点落在x轴正半轴上,②对角线交点落在x轴负半轴上;先求平移后的四边形A1B1C1D1对角线交点E1的坐标,求OE1的长,从而求出结论.
解答 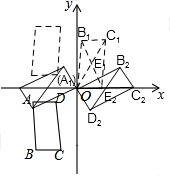 解:由题意得:A1(0,0),C1(6,8),
解:由题意得:A1(0,0),C1(6,8),
根据四个点的坐标可知:四边形ABCD是平行四边形,
∴对角线交点E1是A1C1的中点,
∴E1(3,4),
由勾股定理得:A1E1=$\sqrt{{3}^{2}+{4}^{2}}$=5,
当对角线交点落在x轴正半轴上时,对角线的交点坐标为(5,0),
当对角线交点落在x轴负半轴上时,对角线的交点坐标为(-5,0),
故选D.
点评 本题是坐标与图形变化的问题,关键是能根据题意正确画出图形,根据变化特点确定其各位置点的坐标;要知道:①沿x轴翻折,就是关于x轴对称,沿y轴翻折,就是关于y轴对称;②向右平移a个单位,坐标P(x,y)⇒P(x+a,y),向左平移a个单位,坐标P(x,y)⇒P(x-a,y),向上平移b个单位,坐标P(x,y)⇒P(x,y+b),向下平移b个单位,坐标P(x,y)⇒P(x,y-b).

练习册系列答案
相关题目
4.四个数-5,4,-0.1,$\frac{1}{2}$中最大的数是( )
| A. | -5 | B. | 4 | C. | -0.1 | D. | $\frac{1}{6}$ |
5. 如图,CD∥AB,点F在AB上,EF⊥GF,F为垂足,若∠1=48°,则∠2的度数为( )
如图,CD∥AB,点F在AB上,EF⊥GF,F为垂足,若∠1=48°,则∠2的度数为( )
 如图,CD∥AB,点F在AB上,EF⊥GF,F为垂足,若∠1=48°,则∠2的度数为( )
如图,CD∥AB,点F在AB上,EF⊥GF,F为垂足,若∠1=48°,则∠2的度数为( )| A. | 42° | B. | 45° | C. | 48° | D. | 50° |
2.方程 (x-5)(x-6)=x-5 的解是( )
| A. | x=5 | B. | x=5 或x=6 | C. | x=7 | D. | x=5 或 x=7 |
19.下面四个数中,最大的是( )
| A. | sin88° | B. | $\sqrt{5}-\sqrt{3}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | tan46° |
6.下列计算正确的是( )
| A. | 3x2-x2=3 | B. | 3a2-2a2=a | C. | 3a2-a2=2a2 | D. | 3x2+5x2=8x5 |
3.下列各整式中,次数为5次的单项式是( )
| A. | ab4 | B. | ab5 | C. | a+b4 | D. | a+b5 |
4. 如图,在△ABC中,∠C=45°,AB的垂直平分线交AB于点E,交BC于点D;AC的垂直平分线交AC于点G,交BC与点F,连接AD、AF,若AC=3$\sqrt{2}$,BC=9,则DF等于( )
如图,在△ABC中,∠C=45°,AB的垂直平分线交AB于点E,交BC于点D;AC的垂直平分线交AC于点G,交BC与点F,连接AD、AF,若AC=3$\sqrt{2}$,BC=9,则DF等于( )
 如图,在△ABC中,∠C=45°,AB的垂直平分线交AB于点E,交BC于点D;AC的垂直平分线交AC于点G,交BC与点F,连接AD、AF,若AC=3$\sqrt{2}$,BC=9,则DF等于( )
如图,在△ABC中,∠C=45°,AB的垂直平分线交AB于点E,交BC于点D;AC的垂直平分线交AC于点G,交BC与点F,连接AD、AF,若AC=3$\sqrt{2}$,BC=9,则DF等于( )| A. | $\frac{9}{4}$ | B. | $\frac{7}{2}$ | C. | 4 | D. | $3\sqrt{2}$ |
 重庆实验外国语学校坐落在美丽的“华岩寺”旁边,它被誉为“巴山灵境”.我校实践活动小组准备利用测角器和所学的三角函数知识去测“华岩寺”大佛的高度.他们在A处测得佛顶P的仰角为45°,继而他们沿坡度为i=3:4的斜坡AB前行25米到达大佛广场边缘的B处,BQ∥AC,PQ⊥BQ,在B点测得佛顶P的仰角为63°,则大佛的高度PQ为( )米.
重庆实验外国语学校坐落在美丽的“华岩寺”旁边,它被誉为“巴山灵境”.我校实践活动小组准备利用测角器和所学的三角函数知识去测“华岩寺”大佛的高度.他们在A处测得佛顶P的仰角为45°,继而他们沿坡度为i=3:4的斜坡AB前行25米到达大佛广场边缘的B处,BQ∥AC,PQ⊥BQ,在B点测得佛顶P的仰角为63°,则大佛的高度PQ为( )米.