题目内容
8．用如图甲所示的长方形和正方形纸板做如图乙中竖式和横式两种无盖纸盒，若库存的正方形纸板与长方形纸板的张数分别为420张和930张，做两种纸盒后，库存纸恰好用完，求竖式纸盒和横式纸盒的个数．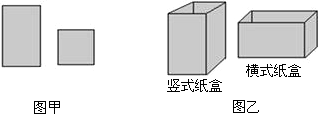
分析 根据图示可得，做一个竖式纸盒需要一张正方形纸板，4张长方形纸板，做一个横式纸盒需要2张正方形纸板，3张长方形纸板，根据正方形纸板与长方形纸板的张数分别为420张和930张，列方程组求解．
解答 解：设竖式纸盒有x个，横式纸盒有y个，
由题意得，$\left\{\begin{array}{l}{x+2y=420}\\{4x+3y=930}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=120}\\{y=150}\end{array}\right.$．
答：竖式纸盒有120个，横式纸盒有150个．
点评 本题考查了二元一次方程组的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程组求解．
练习册系列答案
相关题目
18．
解集在数轴上表示为如图所示的不等式组的是（ ）
解集在数轴上表示为如图所示的不等式组的是（ ）| A． | $\left\{\begin{array}{l}{x＞-1}\\{x≥3}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x＜3}\\{x≤-1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x＜3}\\{x≥-1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x＞3}\\{x≤-1}\end{array}\right.$ |