题目内容
15．
如图，在正三角形网格中，△ABC的顶点都在格点上，点P，Q，M的AB与格线的交点，则△ABC的外心是（ ）| A． | P点 | B． | Q点 | C． | M点 | D． | N点 |
分析 首先证明△ACB是直角三角形，根据直角三角形的外心是斜边的中点即可解决问题．
解答 解：由题意可知，∠BCN=60°，∠ACN=30°，
∴∠ACB=∠ACN+∠BCN=90°，
∴△ABC是直角三角形，
∴△ABC的外心是斜边AB的中点，
∵点Q是AB中点，
∴△ABC的外心是点Q，
故选B．
点评 本题考查三角形的外心与外接圆、等边三角形的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
练习册系列答案
名校课堂系列答案
相关题目
5．一个多边形的每一个外角都等于120°，则这个多边形的边数为（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
6．一元二次方程2x2-5x-4=0的二次项系数、一次项系数及常数项分别是（ ）
| A． | 2，5，-4 | B． | 2，5，4 | C． | 2，-5，-4 | D． | 2，-5，4 |
3．
如图，一束光线从点C出发，经过平面镜AB反射后，沿与AF平行的线段DE射出（此时∠1=∠2），若测得∠DCF=100°，则∠A=（ ）
如图，一束光线从点C出发，经过平面镜AB反射后，沿与AF平行的线段DE射出（此时∠1=∠2），若测得∠DCF=100°，则∠A=（ ）| A． | 50° | B． | 60° | C． | 70° | D． | 80° |
10．已知关于x的不等式组$\left\{\begin{array}{l}{x-a≥b}\\{2x-a＜2b+1}\end{array}\right.$的解集为3≤x＜5，则a、b的值分别为（ ）
| A． | -3，6 | B． | 6，-3 | C． | 1，2 | D． | 0，3 |
20．
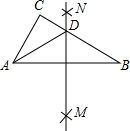如图，在△ABC中，分别以点A和点B为圆心，以大于$\frac{1}{2}$AB的长为半径画弧，两弧相交于点M、N，作直线MN，交BC于点D，若△ADC的周长为10，AB=6，则△ABC的周长为（ ）
如图，在△ABC中，分别以点A和点B为圆心，以大于$\frac{1}{2}$AB的长为半径画弧，两弧相交于点M、N，作直线MN，交BC于点D，若△ADC的周长为10，AB=6，则△ABC的周长为（ ）| A． | 6 | B． | 12 | C． | 16 | D． | 20 |
7．
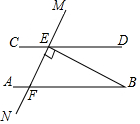如图所示：AB∥CD，MN交CD于点E，交AB于F，BE⊥MN于点E，若∠DEM=55°，则∠ABE=（ ）
如图所示：AB∥CD，MN交CD于点E，交AB于F，BE⊥MN于点E，若∠DEM=55°，则∠ABE=（ ）| A． | 55° | B． | 35° | C． | 45° | D． | 30° |
4．使式子$\sqrt{x-4}$有意义的条件是（ ）
| A． | x≥4 | B． | x=4 | C． | x≤4 | D． | x≠4 |
5．如果一个直角三角形的两边分别是6，8，那么斜边上的中线是（ ）
| A． | 4 | B． | 5 | C． | 4或5 | D． | 3或5 |