题目内容
5．如果一个直角三角形的两边分别是6，8，那么斜边上的中线是（ ）| A． | 4 | B． | 5 | C． | 4或5 | D． | 3或5 |
分析 分一个直角三角形的两直角边分别是6，8和8是斜边两种情况，根据勾股定理、直角三角形的性质计算．
解答 解：当一个直角三角形的两直角边分别是6，8时，
由勾股定理得，斜边=$\sqrt{{6}^{2}+{8}^{2}}$=10，
则斜边上的中线=$\frac{1}{2}×$10=5，
当8是斜边时，斜边上的中线是4，
故选：C．
点评 本题考查的是勾股定理的应用以及直角三角形的性质，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
15．
如图，在正三角形网格中，△ABC的顶点都在格点上，点P，Q，M的AB与格线的交点，则△ABC的外心是（ ）
如图，在正三角形网格中，△ABC的顶点都在格点上，点P，Q，M的AB与格线的交点，则△ABC的外心是（ ）| A． | P点 | B． | Q点 | C． | M点 | D． | N点 |
16．方程组$\left\{\begin{array}{l}2x-y=5\\ 3x-y=7\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}x=3\\ y=1\end{array}\right.$ | B． | $\left\{\begin{array}{l}x=1\\ y=-4\end{array}\right.$ | C． | $\left\{\begin{array}{l}x=2\\ y=-1\end{array}\right.$ | D． | $\left\{\begin{array}{l}x=\frac{12}{5}\\ y=-\frac{1}{5}\end{array}\right.$ |
13．方程4x-3=x的解是（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | 1 | D． | -1 |
20．若a2=25，|b|=3，且ab＞0，则a+b的值为（ ）
| A． | 8 | B． | -8 | C． | 8或-8 | D． | 8或-2 |
10．不等式2（x-1）＞2的解集是（ ）
| A． | x＜0 | B． | x＞1 | C． | x＞2 | D． | x＞3 |
17．
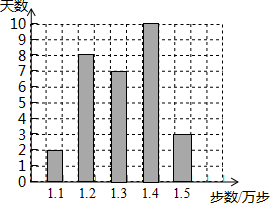李老师用手机软件记录了上个月（30天）每天走路的步数（单位：万步），她将记录的结果绘制成了如图所示的统计图，关于这组数据的众数是（ ）
李老师用手机软件记录了上个月（30天）每天走路的步数（单位：万步），她将记录的结果绘制成了如图所示的统计图，关于这组数据的众数是（ ）| A． | 10 | B． | 1.3 | C． | 1.4 | D． | 1.5 |
14．
如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A，B，C，D的坐标分别是（0，a），（-4，3），（b，m），（c，m），则点E的坐标是（ ）
如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A，B，C，D的坐标分别是（0，a），（-4，3），（b，m），（c，m），则点E的坐标是（ ）| A． | （-4，-3） | B． | （4，3） | C． | （4，-3） | D． | （3，-4） |