题目内容
14．
如图，点C，D是半圆O的三等分点，直径AB=4$\sqrt{3}$．连结AC交半径OD于E，则线段DE，CE以及$\widehat{DC}$围成的封闭图形（即阴影部分）的面积是2π-$\frac{3\sqrt{3}}{2}$．
分析 连接OC，由点C，D是半圆O的三等分点，得到$\widehat{AD}=\widehat{CD}=\widehat{CB}$，根据垂径定理得到OD⊥AC，∠DOC=60°，求得OE=$\sqrt{3}$，CE=6，根据扇形和三角形的面积公式即可得到结论．
解答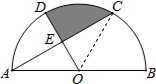 
解：连接OC，
∵点C，D是半圆O的三等分点，
∴$\widehat{AD}=\widehat{CD}=\widehat{CB}$，
∴OD⊥AC，∠DOC=60°，
∴∠OCE=30°，
∵AB=4$\sqrt{3}$，
∴OC=2$\sqrt{3}$
∴OE=$\sqrt{3}$，CE=6，
∴S阴影=S扇形COD-S△OCE=$\frac{60•π•（2\sqrt{3}）^{2}}{360}$-$\frac{1}{2}×6\sqrt{3}$=2$π-\frac{3\sqrt{3}}{2}$．
故答案为：2$π-\frac{3\sqrt{3}}{2}$．
点评 本题考查了扇形的面积的计算，垂径定理，含30°角的直角三角形的性质，正确的识别图形是解题的关键．
练习册系列答案
相关题目
7．
如图，边长为2的等边三角形ABC，点A，B分别在y轴和x轴正半轴滑动，则原点O到C的最长距离（ ）
如图，边长为2的等边三角形ABC，点A，B分别在y轴和x轴正半轴滑动，则原点O到C的最长距离（ ）| A． | $\sqrt{3}-1$ | B． | $\sqrt{5}$ | C． | $\sqrt{2}+1$ | D． | $\sqrt{3}+1$ |
某商场为了吸引顾客设计了一个可以自由转动的转盘，如下图所示，并规定，顾客购买100元的商品，就能获得一次转动转盘的机会，如果转盘停止转动后，指针正好对准红色、黄色、绿色区域，那么顾客就可以分别获得80元、40元、20元的购物券，凭购物券可以在商场继续购物．顾客转动一次转盘时获得三种购物券的可能性各是多大？
如图，已知Rt△ABC中，斜边BC上的高AD=4，tanB=$\frac{3}{4}$，则AC=5．