题目内容
7.在570米环形跑道上,A、B两点相距30米,甲、乙两人分别从A、B两点同时背向出发,两人在C点相遇,相遇后甲的速度提高$\frac{1}{5}$,乙掉头往回走且速度提高$\frac{1}{3}$,甲到A地时乙正好到B地,当甲再追上乙时共跑多少米?分析 根据题意由乙往返走了B到相過点C的长度,由路程一定,时间和速度成反比,可知相遇前和相遇后时间比为(1+$\frac{1}{3}$):1=4:3,进一步得到甲相遇前和相遇后路程比为(4×1):[3×(1+$\frac{1}{5}$)]=10:9,依此可求相遇前甲跑的路程,乙跑的路程,可知原来甲、乙的速度比是300:240=5:4,相遇后它们的速度比是5×(1+$\frac{1}{5}$):4×(1+$\frac{1}{3}$)=9:8,可设甲再追上乙时共跑x米,根据时间一定,路程的比与速度比成正比,路程差的比与速度差的比也成正比,依此列出方程求解即可.
解答 解:相遇前和相遇后时间比为(1+$\frac{1}{3}$):1=4:3,
甲相遇前和相遇后路程比为(4×1):[3×(1+$\frac{1}{5}$)]=10:9,
相遇前甲跑的路程570×$\frac{10}{10+9}$=300(米),
相遇前乙跑的路程570-300-30=240(米),
原来甲、乙的速度比为300:240=5:4,
相遇后它们的速度比5×(1+$\frac{1}{5}$):4×(1+$\frac{1}{3}$)=9:8,
设甲再追上乙时共跑x米,依题意有
(x-300):570=9:(9-8),
解得x=5430.
答:当甲再追上乙时共跑5430米.
点评 考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.本题得到相遇后它们的速度比是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
15.一元二次方程2x2-7x-5=0的两根分别是x1,x2,则x1x2等于( )
| A. | $\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | -$\frac{7}{2}$ | D. | -$\frac{5}{2}$ |
 如图,AB是⊙O的弦,半径OA=20cm,∠AOB=120°.求:
如图,AB是⊙O的弦,半径OA=20cm,∠AOB=120°.求: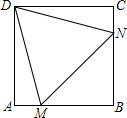 如图,在正方形ABCD中,等边三角形DMN的顶点M、N分别在AB和BC上,若等边三角形DMN的边长为$2\sqrt{2}$,则正方形ABCD的边长为1+$\sqrt{3}$.
如图,在正方形ABCD中,等边三角形DMN的顶点M、N分别在AB和BC上,若等边三角形DMN的边长为$2\sqrt{2}$,则正方形ABCD的边长为1+$\sqrt{3}$.