题目内容
4.先化简$\frac{x+1}{{x}^{2}}$•($\frac{2x}{x+1}$)2-($\frac{1}{x-1}$-$\frac{1}{x+1}$),然后再选择一个你喜欢且使原式有意义的x的值代入化简后的式子求值.分析 原式第一项先计算乘方运算,约分两项通分并利用同分母分式的减法法则计算得到最简结果,把x=2代入计算即可求出值.
解答 解:原式=$\frac{x+1}{{x}^{2}}$•$\frac{4{x}^{2}}{(x+1)^{2}}$-$\frac{x+1-x+1}{(x+1)(x-1)}$
=$\frac{4}{x+1}$-$\frac{2}{(x+1)(x-1)}$
=$\frac{4x-4-2}{(x+1)(x-1)}$
=$\frac{4x-6}{{x}^{2}-1}$,
当x=2时,原式=$\frac{2}{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
15. 如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )
如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )
 如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )
如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
19.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
| A. | 2$\sqrt{5}$cm | B. | 4$\sqrt{5}$cm | C. | 2$\sqrt{5}$cm或4$\sqrt{5}$cm | D. | 2$\sqrt{3}$cm或4$\sqrt{3}$cm |
 如图,矩形ABCD是由三个矩形拼接成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为( )
如图,矩形ABCD是由三个矩形拼接成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为( )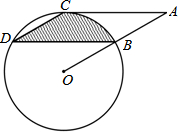 如图,点B,C,D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,BD=4$\sqrt{3}$,则由弦CD,BD与弧BC所围成的阴影部分的面积是$\frac{8}{3}$π.(结果保留π)
如图,点B,C,D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,BD=4$\sqrt{3}$,则由弦CD,BD与弧BC所围成的阴影部分的面积是$\frac{8}{3}$π.(结果保留π) 我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△ADC中,CD=bsinA,AD=bcosA
我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△ADC中,CD=bsinA,AD=bcosA